AVL, Splay and Amortized Analysis

AVL Trees

维持平衡的二叉搜索树，每个节点的左右子树高度差不超过1。

高度平衡

定义空树的高度为 -1

• 空树是高度平衡的

• 一个节点是高度平衡的，当且仅当：

  1. 它的左右子树都是高度平衡的
  2. 它的左右子树的高度差不超过 1

平衡因子（Balance Factor）

对于一个节点，它的平衡因子是它的左子树的高度减去右子树的高度。

即 \( \text{BF}(v) = \text{height}(T_l) - \text{height}(T_r) \)

Operations

树旋转（Tree Rotation）

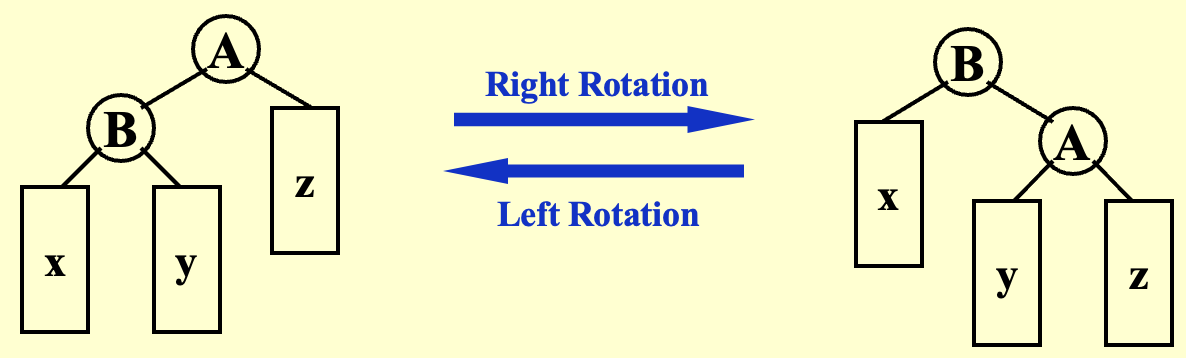
树旋转分为左旋和右旋。旋转操作后，被旋转的边的两端一端的子树高度减小 1，另一端的子树高度增加 1。

参考代码（避免分类讨论）：

/*
 * type = 0: right rotate
 * type = 1: left  rotate
 */
Node *rotate(Node *p, int type) {
    Node *q = p->child[type];
    p->child[type] = q->child[type ^ 1];
    q->child[type ^ 1] = p;
    maintain_info(p);
    maintain_info(q);
    return q;
}

Rebalance

插入和删除操作后，可能会破坏 AVL 树的平衡性。此时需要进行树的旋转操作，使得树重新平衡。

从插入或删除的节点开始，向上回溯更新平衡因子，直到找到第一个不平衡的节点 X。设 X 中高度更高的儿子为 Z，存在四种情况：

• LL：Z 是 X 的左儿子，且 \( \text{BF}(Z) > 1 \)
• LR：Z 是 X 的左儿子，且 \( \text{BF}(Z) < -1 \)
• RR：Z 是 X 的右儿子，且 \( \text{BF}(Z) < -1 \)
• RL：Z 是 X 的右儿子，且 \( \text{BF}(Z) > 1 \)

这里的命名根据的是失衡的来源，而不是旋转操作的顺序

对应的选择操作：

• LL：右旋 X
• LR：左旋 Z，右旋 X
• RR：左旋 X
• RL：右旋 Z，左旋 X

参考代码：

Node *maintain(Node *p) {
    if (p == NULL) return p;
    maintain_info(p);
    if (p->bfactor > 1) {
        if (getHeight(p->child[0]->child[0]) >= getHeight(p->child[0]->child[1])) {
            // LL Rotate
            return rotate(p, 0);
        } else {
            // LR Rotate
            p->child[0] = rotate(p->child[0], 1);
            return rotate(p, 0);
        }
    } else if (p->bfactor < -1) {
        if (getHeight(p->child[1]->child[1]) >= getHeight(p->child[1]->child[0])) {
            // RR Rotate
            return rotate(p, 1);
        } else {
            // RL Rotate
            p->child[1] = rotate(p->child[1], 0);
            return rotate(p, 1);
        }
    }
    return p;
}

Insertion

先递归找到插入的位置，新建节点，然后回溯更新平衡因子，直到找到第一个不平衡的节点，然后进行 rebalance。

Deletion

先递归找到删除的位置，分类讨论：

• 删除的节点只有小于两个儿子：用子节点替换该节点，从此节点开始回溯更新平衡因子。
• 删除的节点有两个儿子：找到该节点的前驱，交换两节点，随后删除前驱节点，从前驱节点开始回溯更新平衡因子。

复杂度分析

设 \( f(h) \) 为高度为 \( h \) 的 AVL 树的最小节点数，那么有：

\[ \begin{aligned} f(-1) = 0, \quad f(0) = 1 \\ f(h) = f(h-1) + f(h-2) + 1 \end{aligned} \]

Fibonacci 数列

Fibonacci 数列的定义为 \( F(0) = 0, F(1) = 1, F(n) = F(n-1) + F(n-2) \)。

其通项公式为：

\[ F(n) \approx \frac{1}{\sqrt{5}} \left( \frac{1 + \sqrt{5}}{2} \right)^n \]

易得 \( f(h) = F(h+3) - 1 \approx \frac{1}{\sqrt{5}} \left( \frac{1 + \sqrt{5}}{2} \right)^{h+3} - 1\)。

则有 \( h = O(\log n) \)，则 AVL 单次操作的时间复杂度为 \( O(\log n) \)。

参考代码

luoguP3369 【模板】普通平衡树

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#define INF INT_MAX
#define max(a, b) ((a) > (b) ? (a) : (b))

typedef struct Node Node;
struct Node {
    int key, height, size, bfactor;
    Node *child[2]; // child[0]: left child, child[1]: right child
};

typedef struct AVLTree AVLTree;
struct AVLTree {
    Node *root;
};

Node *newNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->child[0] = p->child[1] = NULL;
    p->height = 0;
    p->bfactor = 0;
    p->size = 1;
    return p;
}

int getHeight(Node *p) {
    return p == NULL ? -1 : p->height;
}

int getSize(Node *p) {
    return p == NULL ? 0 : p->size;
}

void maintain_info(Node *p) {
    if (p == NULL) return;
    p->height = max(getHeight(p->child[0]), getHeight(p->child[1])) + 1;
    p->bfactor = getHeight(p->child[0]) - getHeight(p->child[1]);
    p->size = 1 + getSize(p->child[0]) + getSize(p->child[1]);
}

/*
* type = 0: right rotate
* type = 1: left  rotate
*/
Node *rotate(Node *p, int type) {
    Node *q = p->child[type];
    p->child[type] = q->child[type ^ 1];
    q->child[type ^ 1] = p;
    maintain_info(p);
    maintain_info(q);
    return q;
}

Node *maintain(Node *p) {
    if (p == NULL) return p;
    maintain_info(p);
    if (p->bfactor > 1) {
        if (getHeight(p->child[0]->child[0]) >= getHeight(p->child[0]->child[1])) {
            // LL Rotate
            return rotate(p, 0);
        } else {
            // LR Rotate
            p->child[0] = rotate(p->child[0], 1);
            return rotate(p, 0);
        }
    } else if (p->bfactor < -1) {
        if (getHeight(p->child[1]->child[1]) >= getHeight(p->child[1]->child[0])) {
            // RR Rotate
            return rotate(p, 1);
        } else {
            // RL Rotate
            p->child[1] = rotate(p->child[1], 0);
            return rotate(p, 1);
        }
    }
    return p;
}

Node *insert(Node *p, int key) {
    if (p == NULL) return newNode(key);
    if (key <= p->key) {
        p->child[0] = insert(p->child[0], key);
    } else {
        p->child[1] = insert(p->child[1], key);
    }
    return maintain(p);
}

Node *erase_max(Node *p) {
    if (p == NULL) return p;
    if (p->child[1] == NULL) {
        Node *q = p->child[0];
        free(p);
        return q;
    } else {
        p->child[1] = erase_max(p->child[1]);
        return maintain(p);
    }
}

Node *erase(Node *p, int key) {
    if (p == NULL) return p;
    if (key < p->key) {
        p->child[0] = erase(p->child[0], key);
    } else if (key > p->key) {
        p->child[1] = erase(p->child[1], key);
    } else {
        if (p->child[0] == NULL || p->child[1] == NULL) {
            Node *q = p->child[0] ? p->child[0] : p->child[1];
            free(p);
            return q;
        } else {
            Node *q = p->child[0];
            while (q->child[1]) q = q->child[1];
            p->key = q->key;
            p->child[0] = erase_max(p->child[0]);
        }
    }
    return maintain(p);
}

int query_rank(Node *p, int key) {
    if (p == NULL) return 0;
    if (key <= p->key) {
        return query_rank(p->child[0], key);
    } else {
        return getSize(p->child[0]) + 1 + query_rank(p->child[1], key);
    }
}

int query_kth(Node *p, int k) {
    if (p == NULL) return INF;
    if (k <= getSize(p->child[0])) {
        return query_kth(p->child[0], k);
    } else if (k == getSize(p->child[0]) + 1) {
        return p->key;
    } else {
        return query_kth(p->child[1], k - getSize(p->child[0]) - 1);
    }
}

int query_pre(Node *p, int key) {
    if (p == NULL) return INF;
    if (key <= p->key) {
        return query_pre(p->child[0], key);
    } else {
        int res = query_pre(p->child[1], key);
        return res == INF ? p->key : res;
    }
}

int query_suc(Node *p, int key) {
    if (p == NULL) return INF;
    if (key >= p->key) {
        return query_suc(p->child[1], key);
    } else {
        int res = query_suc(p->child[0], key);
        return res == INF ? p->key : res;
    }
}

void fprint_tree(Node *p) {
    if (p == NULL) return;
    fprint_tree(p->child[0]);
    fprintf(stderr, "%d ", p->key);
    fprint_tree(p->child[1]);
}

void free_tree(Node *p) {
    if (p == NULL) return;
    free_tree(p->child[0]);
    free_tree(p->child[1]);
    free(p);
}

int main() {
    int n;
    scanf("%d", &n);
    AVLTree *avl = (AVLTree *)malloc(sizeof(AVLTree));
    avl->root = NULL;
    while (n--) {
        int opt, x;
        scanf("%d%d", &opt, &x);
        switch (opt) {
        case 1:
            avl->root = insert(avl->root, x);
            break;
        case 2:
            avl->root = erase(avl->root, x);
            break;
        case 3:
            printf("%d\n", query_rank(avl->root, x) + 1);
            break;
        case 4:
            printf("%d\n", query_kth(avl->root, x));
            break;
        case 5:
            printf("%d\n", query_pre(avl->root, x));
            break;
        case 6:
            printf("%d\n", query_suc(avl->root, x));
            break;
        }
        // fprintf(stderr, "[");
        // fprint_tree(avl->root);
        // fprintf(stderr, "]\n");
    }
    free_tree(avl->root);
    return 0;
}

Splay Trees

自调整二叉搜索树，通过 splay 操作保证复杂度。

Splay 树不一定平衡

Operations

树旋转（Tree Rotation）

Splay 树的旋转操作与 AVL 树类似，还需要额外维护 parent 指针。

参考代码：

// 将 p 向上旋转
void rotate(Node *p) {
    if (p->parent == NULL) return;
    Node *p_parent = p->parent;
    int type = getPosition(p); // 0: left rotate, 1: right rotate
    p_parent->child[type] = p->child[type ^ 1];
    p->child[type ^ 1] = p_parent;
    if (p_parent->parent != NULL) {
        p_parent->parent->child[getPosition(p_parent)] = p;
    }
    p->parent = p_parent->parent;
    p_parent->parent = p;
    if (p_parent->child[type]) {
        p_parent->child[type]->parent = p_parent;
    }
    maintain(p_parent);
    maintain(p);
}

Splay

Splay 操作是将节点通过旋转操作旋转到根节点。

设 x 为要进行 splay 操作的节点，p 为 x 的父节点，g 为 x 的祖父节点，有以下三种情况：

• Zig：p 是根节点，直接旋转 x。

  

• Zig-Zig：p 和 x 在同一侧，先旋转 p，再旋转 x。

  

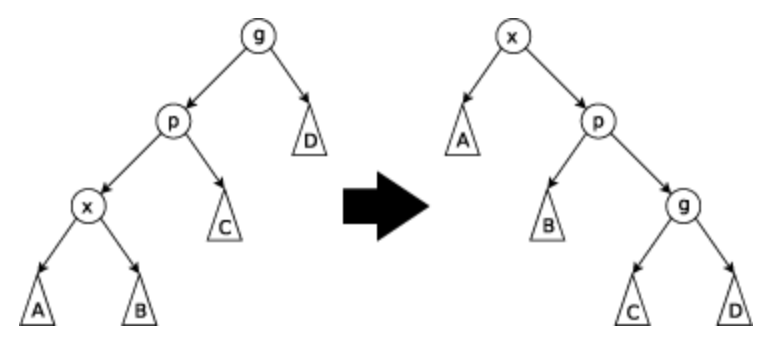
• Zig-Zag：p 和 x 在不同侧，旋转两次 x。

  

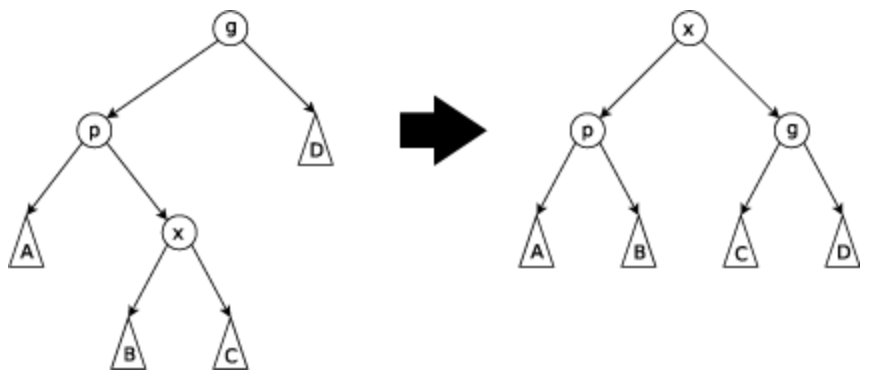
参考代码：

int getPosition(Node *p) {
    if (p->parent == NULL) return -1;
    return p == p->parent->child[1];
}

void splay(SplayTree *tree, Node *p) {
    for (Node *par = p->parent; par != NULL; rotate(p), par = p->parent) {
        if (par->parent != NULL) {
            rotate(getPosition(p) == getPosition(par) ? par : p);
        }
    }
    tree->root = p;
}

Insertion

先递归找到插入的位置，新建节点，然后 splay 该节点。

Merge

合并两棵 splay 树，且保证左树的所有节点的键值小于右树的所有节点的键值。

先对左树中最大的节点进行 splay 操作，然后将右树作为左树根节点的右子树。

Deletion

先递归找到删除的位置，将其 splay 到根节点，然后删除根节点，再将左右子树合并。

参考代码

luoguP3369 【模板】普通平衡树

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#define INF INT_MAX
#define max(a, b) ((a) > (b) ? (a) : (b))

typedef struct Node Node;
struct Node {
    int key, size, cnt;
    Node *child[2]; // child[0]: left child, child[1]: right child
    Node *parent;
};

typedef struct SplayTree SplayTree;
struct SplayTree {
    Node *root;
};

// void fprint_tree(Node *p) {
//     if (p == NULL) return;
//     fprint_tree(p->child[0]);
//     fprintf(stderr, "%d(%d, par:%d)[%d, %d] ", p->key, p->cnt, p->parent != NULL ? p->parent->key : -1,
//                 p->child[0] != NULL ? p->child[0]->key : -1, p->child[1] != NULL ? p->child[1]->key : -1);
//     fprint_tree(p->child[1]);
// }

Node *newNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->size = 1;
    p->cnt = 1;
    p->child[0] = p->child[1] = NULL;
    p->parent = NULL;
    return p;
}

int getSize(Node *p) {
    return p == NULL ? 0 : p->size;
}

int getPosition(Node *p) {
    if (p->parent == NULL) return -1;
    return p == p->parent->child[1];
}

void maintain(Node *p) {
    if (p == NULL) return;
    p->size = p->cnt + getSize(p->child[0]) + getSize(p->child[1]);
}

void rotate(Node *p) {
    if (p->parent == NULL) return;
    Node *p_parent = p->parent;
    int type = getPosition(p); // 0: left rotate, 1: right rotate
    p_parent->child[type] = p->child[type ^ 1];
    p->child[type ^ 1] = p_parent;
    if (p_parent->parent != NULL) {
        p_parent->parent->child[getPosition(p_parent)] = p;
    }
    p->parent = p_parent->parent;
    p_parent->parent = p;
    if (p_parent->child[type]) {
        p_parent->child[type]->parent = p_parent;
    }
    maintain(p_parent);
    maintain(p);
}

void splay(SplayTree *tree, Node *p) {
    for (Node *par = p->parent; par != NULL; rotate(p), par = p->parent) {
        if (par->parent != NULL) {
            rotate(getPosition(p) == getPosition(par) ? par : p);
        }
    }
    tree->root = p;
}

void insert(SplayTree *tree, int key) {
    if (tree->root == NULL) {
        tree->root = newNode(key);
        return;
    }
    Node *p = tree->root, *par = NULL;
    while (p != NULL) {
        par = p;
        if (key < p->key) {
            p = p->child[0];
        } else if (key > p->key) {
            p = p->child[1];
        } else {
            p->cnt++;
            maintain(p);
            splay(tree, p);
            return;
        }
    }
    p = newNode(key);
    p->parent = par;
    if (key <= par->key) {
        par->child[0] = p;
    } else {
        par->child[1] = p;
    }
    splay(tree, p);
}

int query_kth(SplayTree *tree, int k) {
    Node *p = tree->root;
    while (p != NULL) {
        if (k <= getSize(p->child[0])) {
            p = p->child[0];
        } else if (k > getSize(p->child[0]) + p->cnt) {
            k -= getSize(p->child[0]) + p->cnt;
            p = p->child[1];
        } else {
            break;
        }
    }
    if (p == NULL) return INF;
    splay(tree, p);
    return p->key;
}

void erase(SplayTree *tree, int key) {
    Node *p = tree->root;
    while (p != NULL) {
        if (key == p->key) {
            break;
        } else if (key < p->key) {
            p = p->child[0];
        } else {
            p = p->child[1];
        }
    }
    if (p == NULL) return;
    splay(tree, p);
    if (p->cnt > 1) {
        p->cnt--;
        maintain(p);
        return;
    } else if (p->child[0] == NULL || p->child[1] == NULL) {
        Node *q = p->child[0] ? p->child[0] : p->child[1];
        if (q != NULL) {
            q->parent = NULL;
        }
        free(p);
        tree->root = q;
        return;
    } else {
        p->child[0]->parent = p->child[1]->parent = NULL;
        tree->root = p->child[0];
        query_kth(tree, getSize(p->child[0]));
        tree->root->child[1] = p->child[1];
        p->child[1]->parent = tree->root;
        maintain(tree->root);
    }
}

int query_rank(SplayTree *tree, int key) {
    insert(tree, key);
    int res = getSize(tree->root->child[0]) + 1;
    erase(tree, key);
    return res;
}

int query_pre(SplayTree *tree, int key) {
    insert(tree, key);
    int res = query_kth(tree, getSize(tree->root->child[0]));
    erase(tree, key);
    return res;
}

int query_suc(SplayTree *tree, int key) {
    insert(tree, key);
    int res = query_kth(tree, getSize(tree->root->child[0]) + tree->root->cnt + 1);
    erase(tree, key);
    return res;
}

void free_tree(Node *p) {
    if (p == NULL) return;
    free_tree(p->child[0]);
    free_tree(p->child[1]);
    free(p);
}

int main() {
    int n;
    scanf("%d", &n);
    SplayTree *tree = (SplayTree *)malloc(sizeof(SplayTree));
    tree->root = NULL;
    while (n--) {
        int opt, x;
        scanf("%d%d", &opt, &x);
        switch (opt) {
        case 1:
            insert(tree, x);
            break;
        case 2:
            erase(tree, x);
            break;
        case 3:
            printf("%d\n", query_rank(tree, x));
            break;
        case 4:
            printf("%d\n", query_kth(tree, x));
            break;
        case 5:
            printf("%d\n", query_pre(tree, x));
            break;
        case 6:
            printf("%d\n", query_suc(tree, x));
            break;
        }
        // fprintf(stderr, "[");
        // fprint_tree(tree->root);
        // fprintf(stderr, "]\n");
    }
    free_tree(tree->root);
    return 0;
}

Amortized Analysis 摊还分析

由于程序不一定每次操作都达到最坏的复杂度，因此使用最坏复杂度估计复杂度上界可能会远远高于实际的复杂度，所以需要一种方法来更加精确地估计复杂度上界。

\[ \text{worst-case bound} \geq \text{amortized bound} \geq \text{average-case bound} \]

Aggregate Analysis 聚合分析

考虑操作的整体，设 \(n\) 个操作的复杂度之和为 \(T(n)\)，则单个操作的均摊复杂度为 \(T(n)/n\)。

Accounting Method 核算法

若某次操作的摊还代价 \(\hat{c}_i\) 超过了实际代价 \(c_i\)，则记多出来的部分为“信用分”（credit）。若之后的操作的摊还代价不足以支付实际代价，则使用信用分来支付。则单次操作的均摊复杂度为：

\[ T_{\text{amortized}} = \frac{\sum \hat{c}_i}{n} \geq \frac{\sum c_i}{n} \]

Potential Method 势能法

设 \(D_i\) 为第 \(i\) 次操作之后数据整体的状态，构造函数 \(\Phi(D_i)\) 作为数据状态的“势能”，且满足：

• \(\Phi(D_0) = 0\)
• \(\Phi(D_i) \geq 0\)

由此，摊还代价为：

\[ \hat{c}_i = c_i + \Phi(D_i) - \Phi(D_{i-1}) \]

\(n\) 次操作总代价为：

\[ \begin{aligned} \sum_{i=1}^n \hat{c}_i &= \sum_{i=1}^n (c_i + \Phi(D_i) - \Phi(D_{i-1})) \\ &= \sum_{i=1}^n c_i + \Phi(D_n) - \Phi(D_0) \\ \end{aligned} \]

得到 \(n\) 次操作的总时间复杂度为 \(T(n) = \sum_{i=1}^n c_i + \Phi(D_n) - \Phi(D_0)\)。单次操作时间复杂度为 \(T(n)/n\)。

Warning

势能函数必须满足 \( \Phi(D_n) \geq \Phi(D_0) \)，即初始状态的势能最小，一般将其取为 0。

注意 \( \Phi(D_n) \) 是完整操作之后的势能，最后得出的时间复杂度就是完整操作的复杂度，而其子操作带来的势能变化不用考虑。即可能存在 \( \Phi(D_i) < \Phi(D_0) \)，但只要满足 \( \Phi(D_n) \geq \Phi(D_0) \) 即可。

Splay 复杂度证明

设 \(D_i\) 为第 \(i\) 次操作之后的 Splay 树，\(S(x)\) 为以节点 \(x\) 为根的子树大小，定义势能函数为：

\[ \Phi(T) = \sum_{x \in T} \log S(x) \]

下面对三种操作进行分类讨论，设 \(R_1(x)\) 为操作前以 \(x\) 为根的子树大小的对数，\(R_2(x)\) 为操作后以 \(x\) 为根的子树大小的对数。

用到的不等式

若 \( a+b \leq c \)，则有：

\[ \log a + \log b \leq 2\log c - 2 \]

证明

由 \( ab \leq \frac{1}{4} (a + b)^2 \)，得

\[ \begin{aligned} \log a + \log b &= \log(ab) \\ &\leq \log \frac{1}{4} + 2\log(a+b) \\ &\leq 2\log c - 2 \end{aligned} \]

ZigZig-ZagZig-Zig

\[ \begin{aligned} \hat{c}_i &= 1 + R_2(x) - R_1(x) + R_2(p) - R_1(p) \\ &\leq 1 + R_2(x) - R_1(x) \end{aligned} \]

\[ \begin{aligned} \hat{c}_i &= 2 + R_2(x) - R_1(x) + R_2(p) - R_1(p) + R_2(g) - R_1(g) \\ &\leq 2 - R_1(x) + R_2(p) - R_1(p) + R_2(g) \\ &= 2 - R_1(x) - R_1(p) + (R_2(p) + R_2(g)) \\ &\leq - 2R_1(x) + 2R_2(x) \\ &= 2(R_2(x) - R_1(x)) \\ &\leq 3(R_2(x) - R_1(x)) \end{aligned} \]

\[ \begin{aligned} \hat{c}_i &= 2 + R_2(x) - R_1(x) + R_2(p) - R_1(p) + R_2(g) - R_1(g) \\ &\leq 2 - 2R_1(x) + R_2(p) - R_1(p) + (R_1(x) + R_2(g)) \\ &\leq - 2R_1(x) + R_2(x) - R_1(x) + 2R_2(x) \\ &= 3(R_2(x) - R_1(x)) \end{aligned} \]

由此可得，单次 AVL 操作（insert，delete，e.t.c）的均摊复杂度为

\[ T \leq 1 + 3(R_m(root) - R_0(x)) = O(\log n) \]