Binomial Queue¶
Definition¶
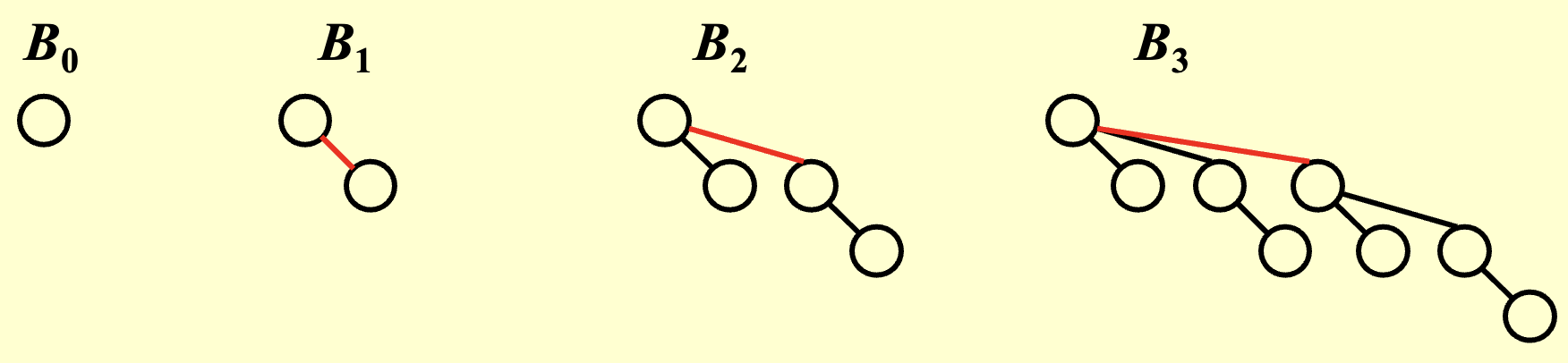
二项队列由一组二项树组成。度为 \(k\) 的二项树满足:
- 满足堆序性质。
- 有 \(2^k\) 个节点。
- 根节点有 \(k\) 棵子树,分别是度为 \(0, 1, \ldots, k-1\) 的二项树。
Operations¶
Merge¶
Merge Trees¶
合并两棵二项树,要求度必须相等。
选择键值较小的根节点作为新根节点,然后将另一二项树作为新根节点的子树。
Merge Queues¶
二项树的度和二项队列节点数的关系
假设 \(n\) 的二进制表示为 \(b_k b_{k-1} \ldots b_0\),则节点数为 \(n\) 的二项队列,若 \(b_i = 1\),则包含度为 \(i\) 的二项树。
类似二进制加法,同度的二项树合并,若产生进位,则合并到度更高的二项树。
Insertion¶
将新节点作为度为 \(0\) 的二项树,然后与原二项队列合并。
Deletion¶
找到根节点键值最小的二项树,删除根节点,然后将其子树作为一个新的二项队列,与原二项队列合并。
Complexity Analysis¶
二项树合并的时间复杂度为 \(O(1)\),单次二项队列合并的时间复杂度为 \(O(\log n)\)。
Amortized Analysis¶
对于一个空的二项队列,插入 \(n\) 个节点。
设 \(c_i, c'_i\) 分别表示插入 \(i\) 个节点的实际代价和均摊代价,势能函数 \(\Phi_i\) 定义为第 \(i\) 次插入后二项队列中二项树的个数。
Note
实际代价为 \(c\) 的一次插入会导致势能增加 \(2-c\)。分类讨论:
- 若插入不产生进位,实际代价为 \(1\),势能增加 \(1\)。
- 若插入产生进位,进位次数为 \(k\),实际代价为 \(k+1\),势能增加 \(1-k\)。
有 \(c'_i = c_i + \Phi_{i+1} - \Phi_i = 2\),即总代价为 \(T(n) = 2n\),均摊代价为 \(O(1)\)。