Combinational Logic Design¶

Combinational Logic¶

Functions and Functional Blocks¶

verilog 中，调用模块会在电路中增加实例，会增加开销。

verilog 中并行运行。

Multiple-bit Rudiementary Functions¶

A wide line is used to represent a bus (总线). The bus can be split into individual lines.

Enable Function¶

与门 + 非门

Decoding 译码¶

the conversion of an n-bit input code to an m-bit output code with \(n \leq m \leq 2^n\) such that each valid code word produces a unique output code

Example:

1-to-2-line decoder
2-to-4-line decoder

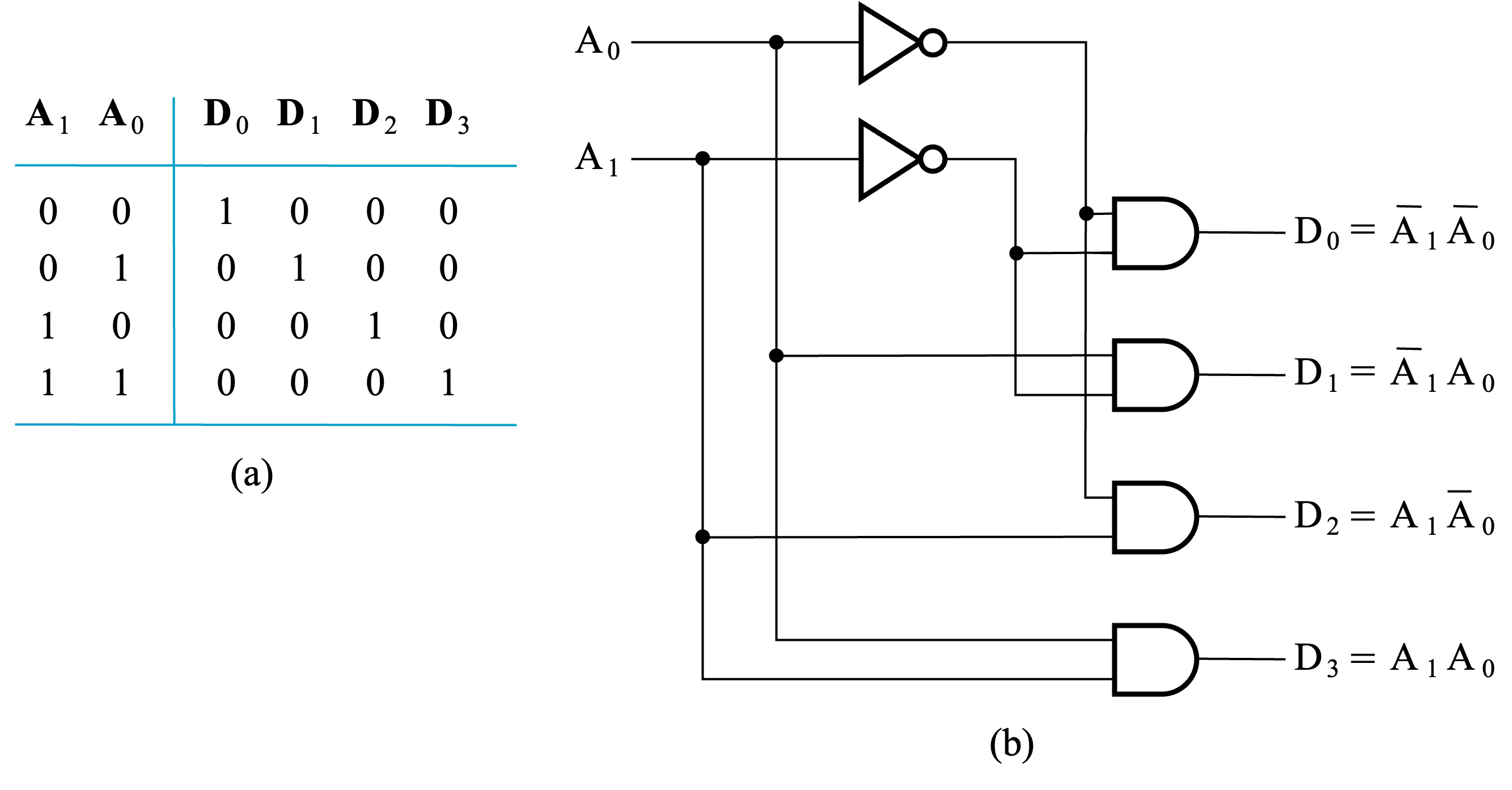
行列译码器：将输入不断二分，例如 4-to-16 拆成 2-to4 和 2-to-4，再将 2-to-4 拆成 1-to-2 和 1-to-2。

Logic Functions Implementation¶

实现任意逻辑函数：译码器 + 或门

译码器输出是所有最小项，通过或门实现逻辑函数。

BCD-to-Segment Decoder¶

Implement:

Common anode 共阳极:
- 控制亮：LED 另一级接低电平(0)
- 控制灭：LED 另一级接高电平(1)
Common cathode 共阴极
- 控制亮：LED 另一级接高电平(1)
- 控制灭：LED 另一级接低电平(0)

Encoding 编码¶

the conversion of an m-bit input code to an n-bit output code with \(m \geq n\) such that each valid code word produces a unique output code (index to code)

Decimal-to-BCD Encoder¶

Input: 10 bits (0-9)
Output: 4 bits (0000-1001)
Function: if input bit \(D_i\) is 1, then output \((A_3, A_2, A_1, A_0)\) is the BCD code for \(i\).

Commonly don't use truth table.

Equations:

\[\begin{align} A_0 &= D_1 + D_3 + D_5 + D_7 + D_9 \\ A_1 &= D_2 + D_3 + D_6 + D_7 \\ A_2 &= D_4 + D_5 + D_6 + D_7 \\ A_3 &= D_8 + D_9 \end{align}\]

Priority Encoder¶

Accepts multiple inputs and use the highest priority input.

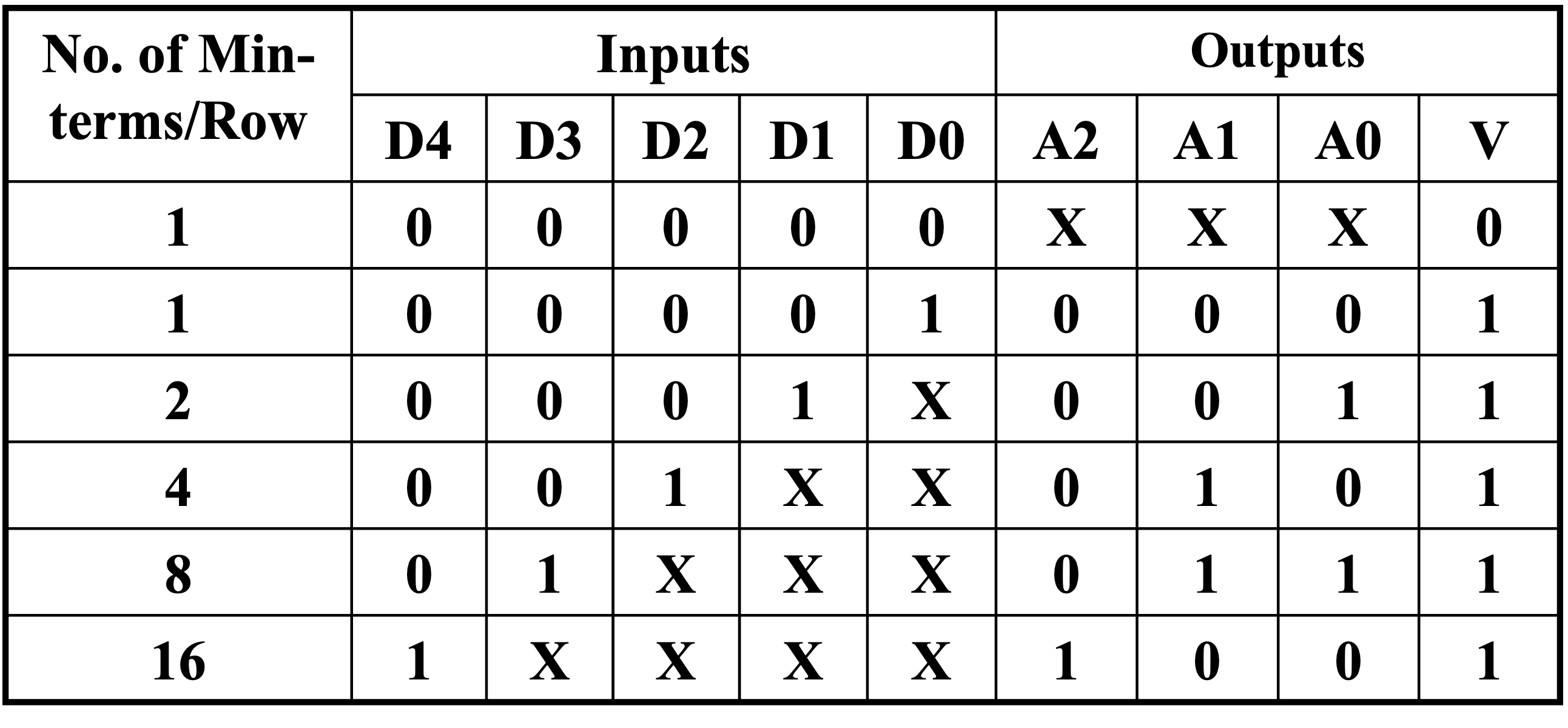
where \(V\) indicates at least one 1 present.

Use K-map to get equations:

\[\begin{align} F_1 &= D_3 + D_2 \\ A_2 &= D_4 \\ A_1 &= \bar D_4 D_3 + \bar D_4 \bar D_3 D_2 = \bar D_4 F_1 \\ A_0 &= \bar D_4 D_3 + \bar D_4 \bar D_3 \bar D_2 D_1 = \bar D_4 (D_3 + \bar D_2 D_1) \\ V &= D_4 + F_1 + D_1 + D_0 \end{align}\]

Multiplexers 多路选择器¶

A multiplexer selects information from an input line and directs the information to an output line.

Decoder + Enable.

2-to-1-line Multiplexer¶

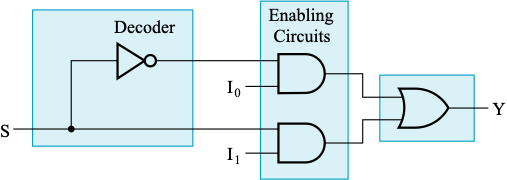
4-to-1-line Multiplexer¶

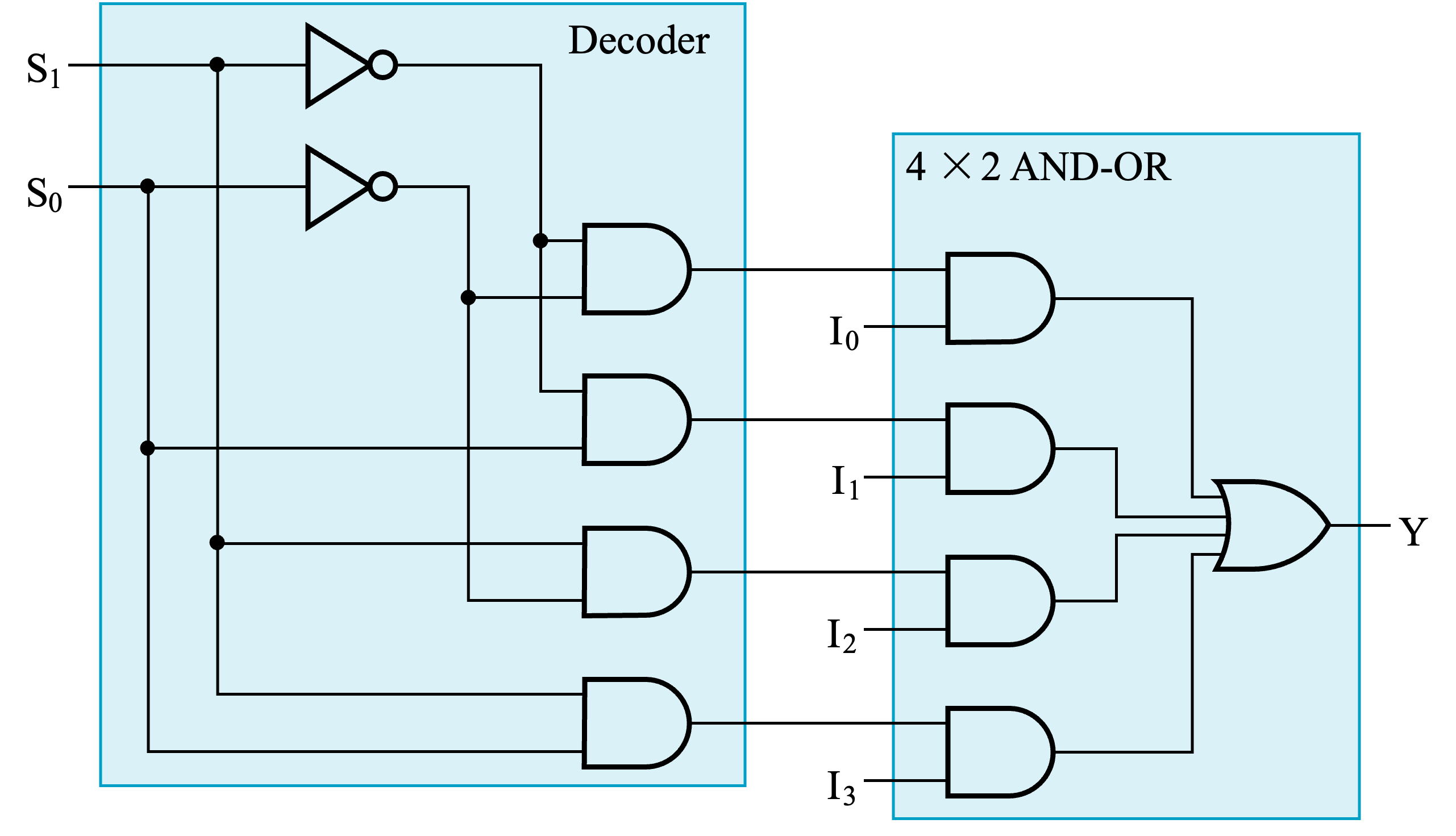
Multiplexer Width Expansion¶

Select "vector bits" instead of "bits".

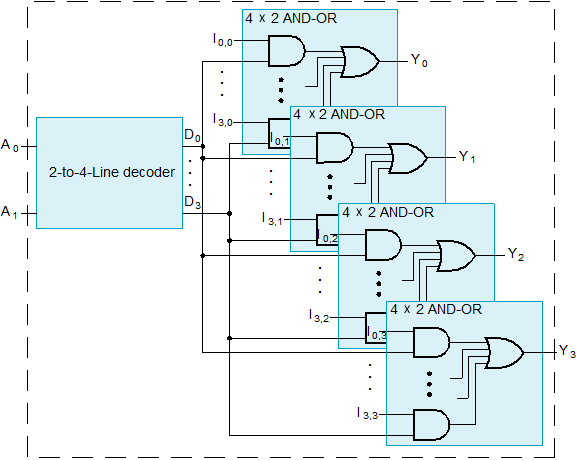
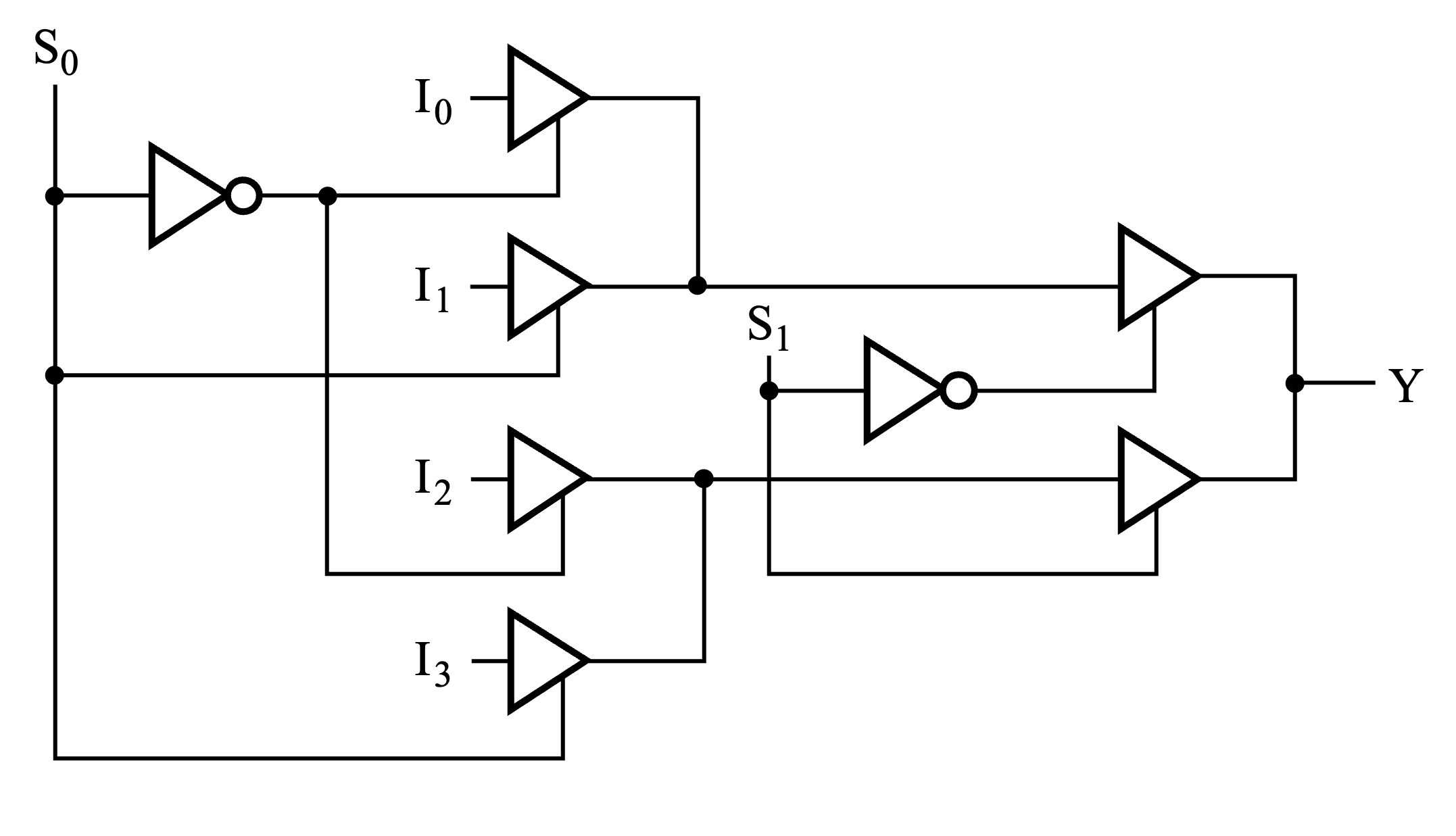
Other Multiplexers¶

Use three-state drivers.

Combinational Logic Implementation¶

Multiplexer Approach 1¶

n inputs, m outputs

Use m-width \(2^n\)-to-1-line multiplexer

Gray to Binary Code

Truth table:
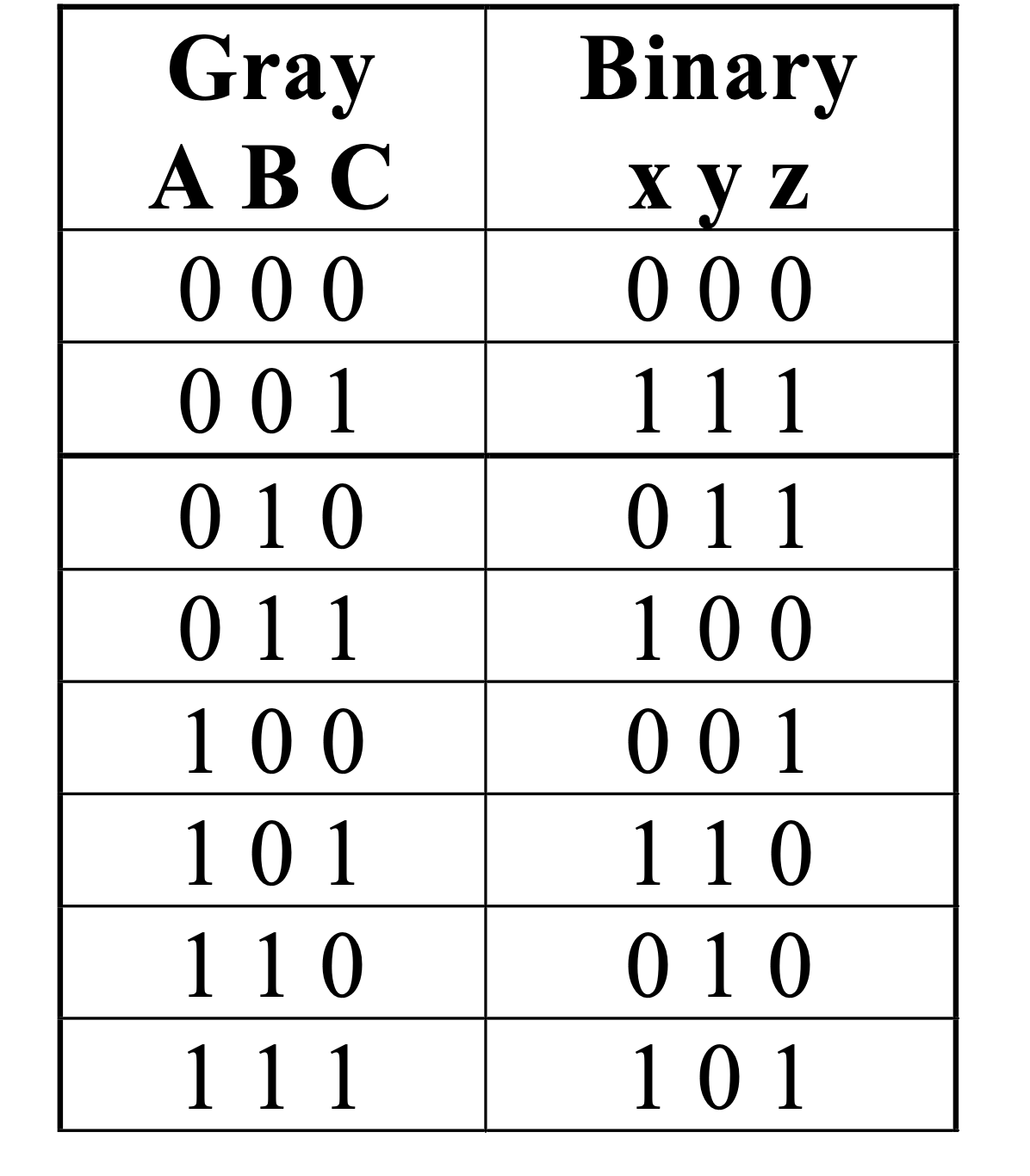
Mux:

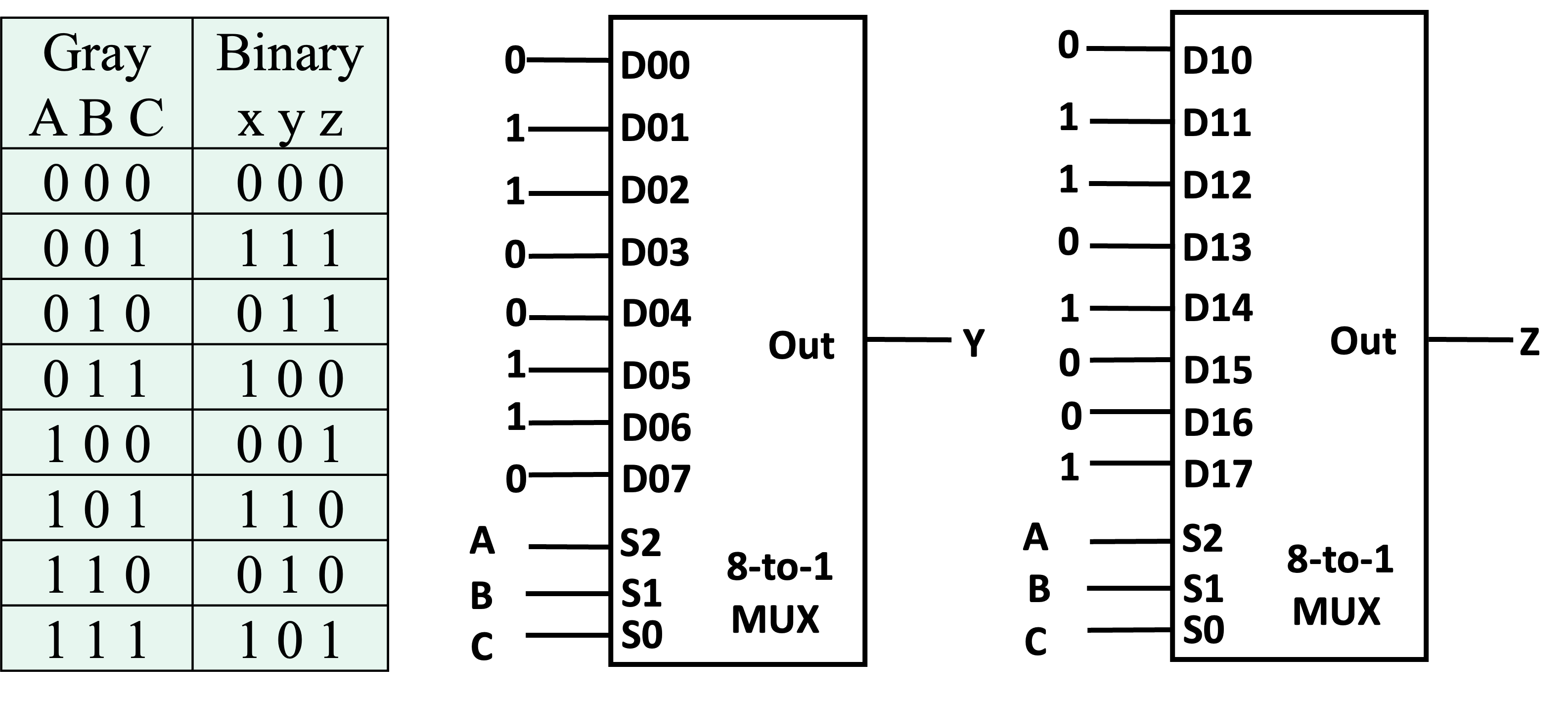
Multiplexer Approach 2¶

n + 1 inputs, m outputs

Use m-width \(2^n\)-to-1-line multiplexer.

Design:

Find the truth table for the function.
Based on the values of the first n variables, separate the truth table rows into pairs. 根据前 n 个变量的值，将真值表分成两行一对。
For each pair and output, define a rudimentary function of the final variable \((0, 1, X, \bar X)\)
Use the first n variables as the select inputs of a multiplexer and the rudimentary functions as the data inputs.

Gray to Binary Code

Truth table:
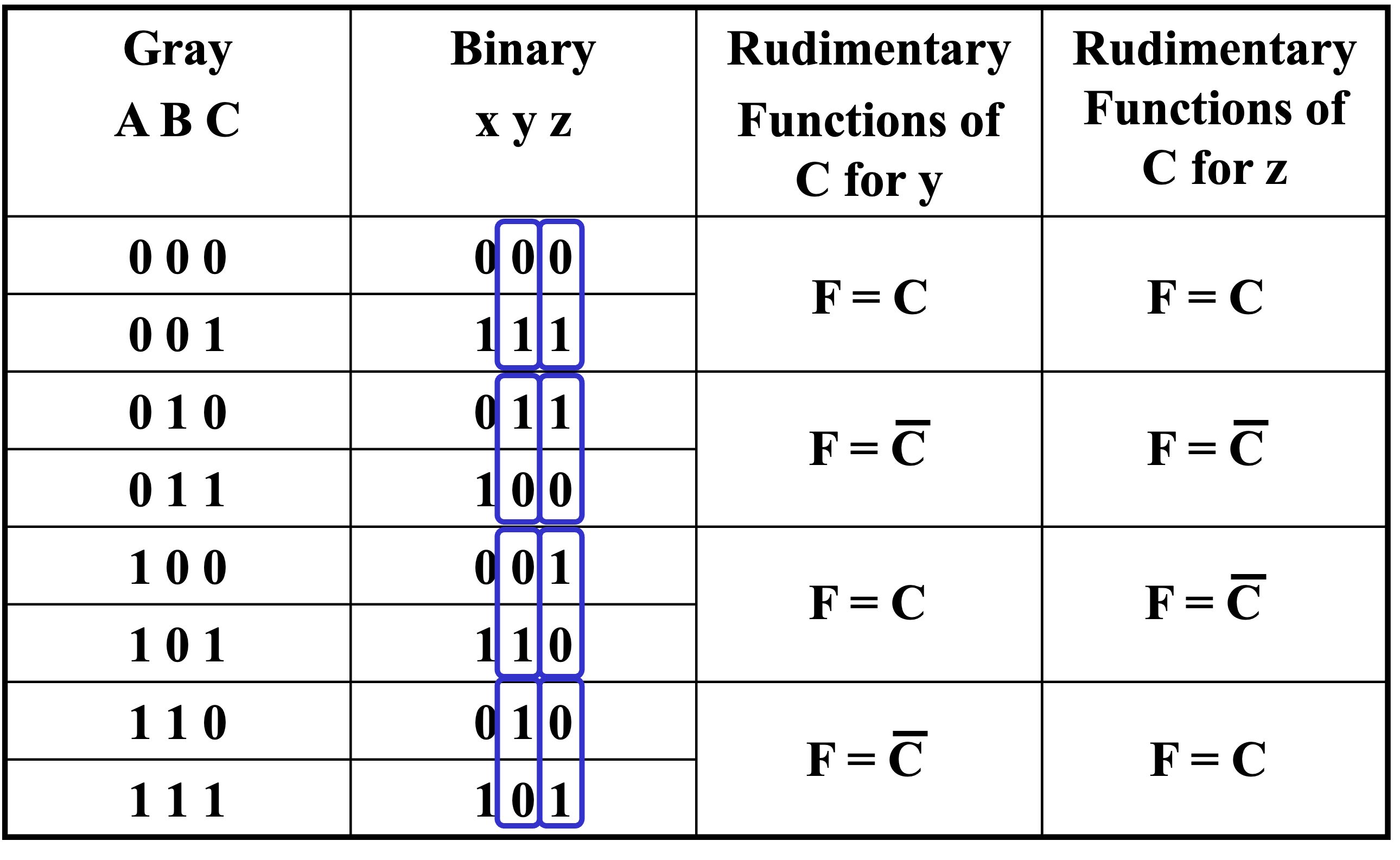
Mux:

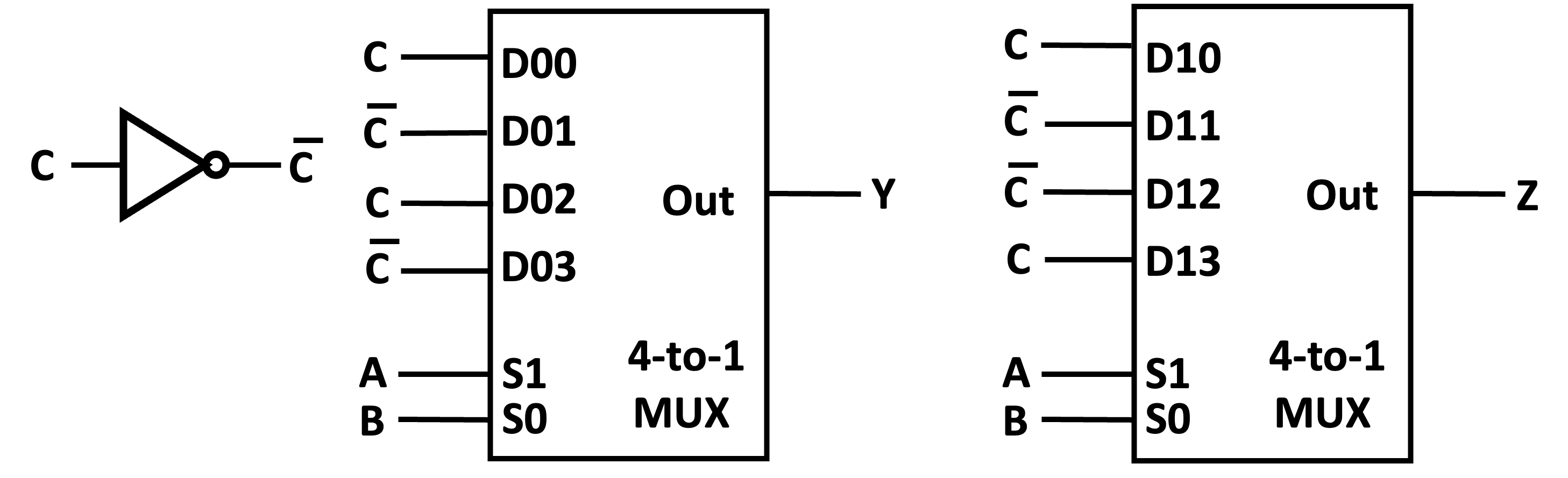
Design Procedure¶

Combinational Circuits¶

输入与输出严格对应

Beginning Hierarchical Design¶

Top-Down: 从顶层开始设计，逐步细化
Bottom-Up: 从最底层开始设计，逐步合并

Design Procedure¶

Specification 简化
Formulation 公式化

Derive a truth table or initial Boolean equations for each output function.

Apply hierarchical design to the output functions.
Optimization 优化

Apply multiple-level logic optimization to the output functions.

Draw logic diagrams.
Technology Mapping 技术映射

Map the logic diagrams into a specific technology.
Verification 验证

Verify the design by simulation.

Design BCD to Excess-3 Code Converter

Specification
- BCD code words for digits 0 through 9 are 0000 through 1001, respectively.
- Excess-3 code words for digits 0 through 9 consisting of 3 added to the BCD code words.
Formulation

write truth table (A-F 无关项)

Input BCD: ABCD, Output Excess-3: WXYZ
Optimization
1. Use K-maps:
  
  \[\begin{align} W &= A + BC + BD \\ X &= \bar BC + \bar BD + B\bar C\bar D \\ Y &= CD + \bar C \bar D \\ Z &= \bar D \end{align}\]
  
  G = 23
2. Multiple-level logic optimization
  
  \(T_1 = C + D\), then
  
  \[\begin{align} T_1 = C + D , G &&= 2 \\ \bar T_1 , G &&= 1 \\ W &= A + B(T_1) , G &&= 4 \\ X &= \bar B(T_1) + B\bar T_1 , G &&= 6 \\ Y &= CD + \bar T_1 , G &&= 4 \\ Z &= \bar D, G &&= 0 \end{align}\]
  
  G = 17
3. Technology mapping
  
  Convert to NAND gates or NOR gates.

Chip Design Styles¶

Full custom: 为特定应用设计

优点：最小面积，最快速度，生产成本低

缺点：设计周期长，设计成本高
Standard cell: 包含标准模块（类似标准库）

优点：设计周期短，设计成本低

缺点：面积大，速度慢，生产成本高
Gate array: 门阵列（可编程）

优点：成本最低

缺点：面积大，速度慢

Cell Libraries¶

Cell: pre-designed logic block
Cell library: a collection of cells
Cell characterization: a detailed specification of the cell for use.

Cell Library

Mapping to NAND gate¶

Convert any circuits to NAND gates.

Assumptions

Gate loading and delay are ignored.
可以用任意多输入的 NAND 门

Convert AND and OR gates to NAND gates
- \(A + B = \overline{\overline{A + B}} = \overline{\bar A \bar B}\)
- \(AB = \overline{\overline{AB}}\)
Pushing inverters through circuit fan-out points

Mapping to NOR is similar.

Verificaiton¶

Manual Logic Analysis (Simple Circuits)
- Write a truth table.
- Derive Boolean equations.
Simulation
1. Write a test program.
2. Simulate the circuit.
apply all possible input combinations or important input combinations

Arithmetic Functions¶

Iterative Combinational Circuits¶

Use blocked diagram to process each bit.

Half Adder¶

inputs: \(X, Y\); outputs: \(S, C\) (sum, carry)

\[\begin{align} S &= A \oplus B \\ C &= AB \end{align}\]

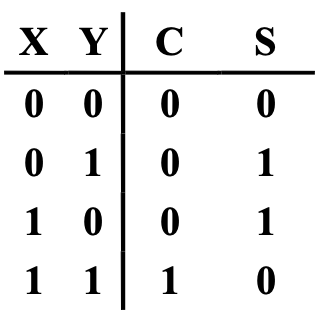
Full Adder¶

inputs: \(X, Y, Z\) (\(Z\): carry); outputs: \(S, C\)

\[\begin{align} S &= X \oplus Y \oplus Z \\ C &= XY + XZ + YZ = XY + (X \oplus Y)Z \end{align}\]

Implement:

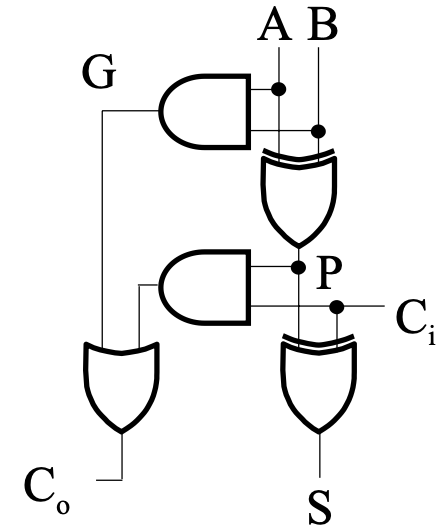
\[\begin{align} G = XY, P = X \oplus Y \\ S = P \oplus Z, C = G + PZ \end{align}\]

4-bit Ripple-Carry Adder¶

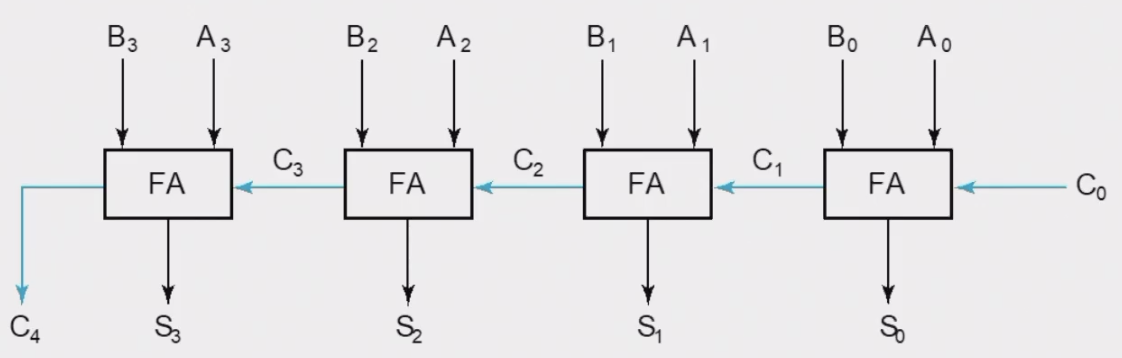
缺点：延迟高（Carry 需要传递）

Carry Lookahead

\(P_i = X_i \oplus Y_i, G_i = X_iY_i\)

\(C_4 = G_3 + P_3G_2 + P_3P_2G_1 + P_3P_2P_1G_0 + P_3P_2P_1P_0C_0\)

缺点：门输入成本大、扇出系数大导致延迟高，随着位数增加，成本大大增加

Group Carry Lookahead Logic

16-bit adder: 4 groups

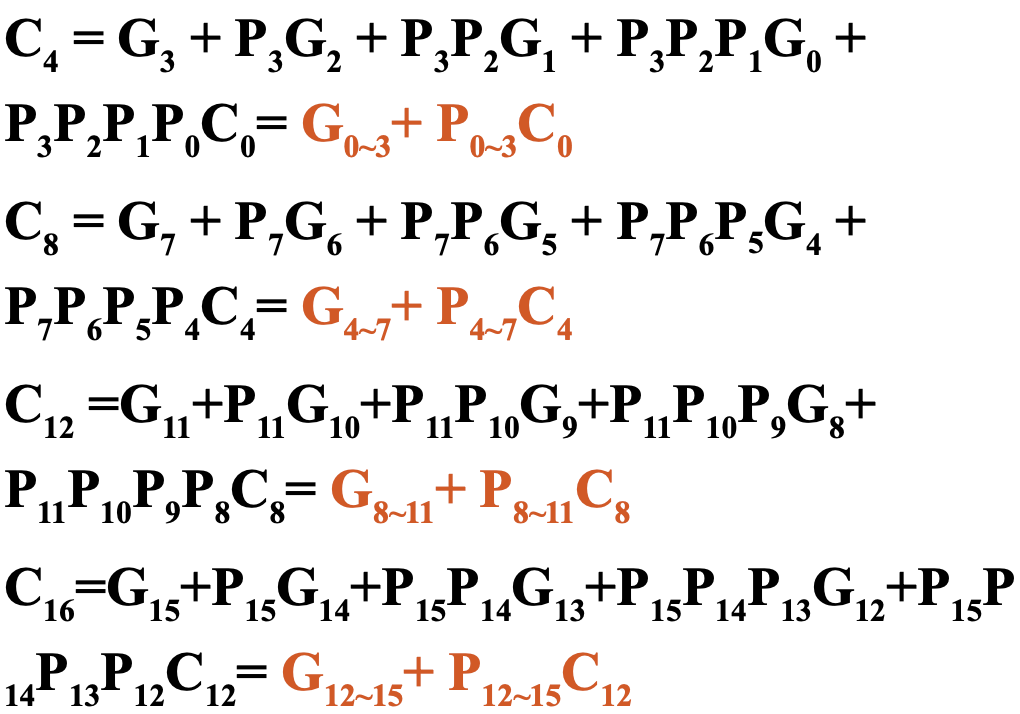
\[\begin{align} G_{0\sim 3} &= G_3 + P_3G_2 + P_3P_2G_1 + P_3P_2P_1G_0 \\ P_{0\sim 3} &= P_3P_2P_1P_0 \end{align}\]

CLA: input \(G_0, P_0, G_1, P_1, G_2, P_2, G_3, P_3\), output \(G_{0\sim 3}, P_{0\sim 3}\)

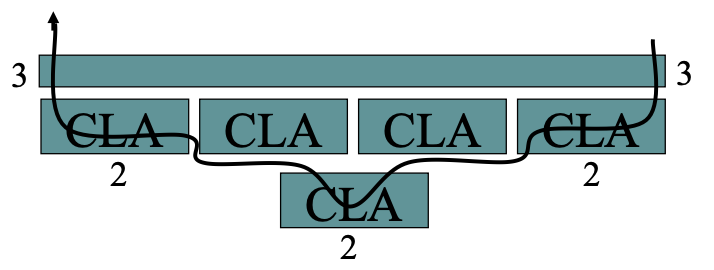
第一层最右 CLA: input \(G_0, P_0, G_1, P_1, G_2, P_2, G_3, P_3\), output \(G_{0\sim 3}, P_{0\sim 3}\)

第二层 CLA: input \(C_0, G_{0\sim 3}, P_{0\sim 3}, G_{4\sim 7}, P_{4\sim 7}, G_{8\sim 11}, P_{8\sim 11}, G_{12\sim 15}, P_{12\sim 15}\), output \(C_4, C_8, C_{12}, C_{16}\)

Longest Delays:

\(A_0, B_0 \to CLA \to G_0, P_0 \to CLA \to C_{12} \to CLA \to C_{16}\)

Unsigned Subtraction¶

Note

compute: \(N - M\)

\(N \geq M\): 无借位
\(N < M\): \(N - M = -(2^n - (M - N))\) 最高位借位

一般不用这种方法。

2's Complements:

Diminished Radix Complement (DRC) 反码 \(2^n - M - 1\)
Radix Complement (RC) 补码 \(2^n - M\)

\(M - N = M + (2^n - N)\) (n-bit)

\(M \geq N\): \(2^n\) 溢出，\(M - N\) 保留
\(M < N\): 结果为负数，求得补码。

如果有进位，则说明结果为正数，无借位；否则结果为负数，有借位。

Signed Integer¶

最高位是符号位，0 表示正数，1 表示负数。一般采用 2's Complements 即符号位+补码。

电路中的实现

加法：直接相加
减法：将减数取反加一（变为减数取反之后的补码），再与被减数相加

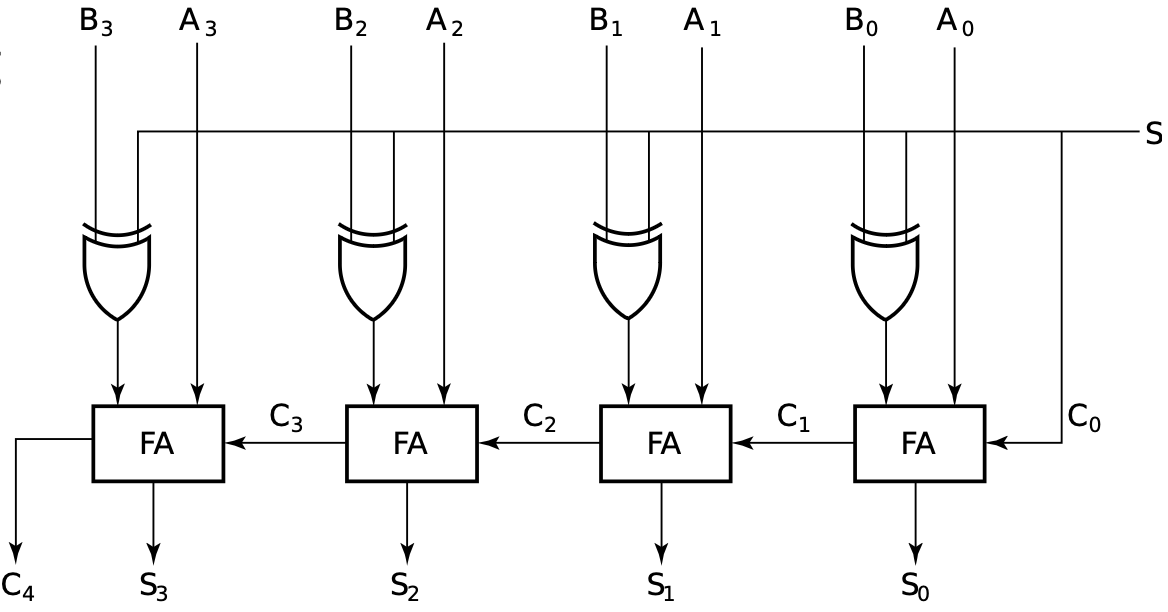
Overflow Detection¶

通过符号位判断溢出，有 8 种情况：

无溢出
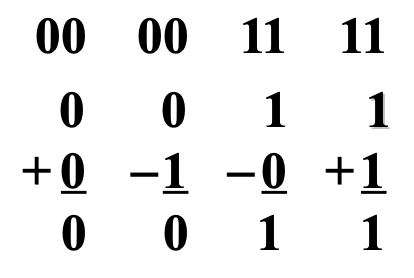
有溢出

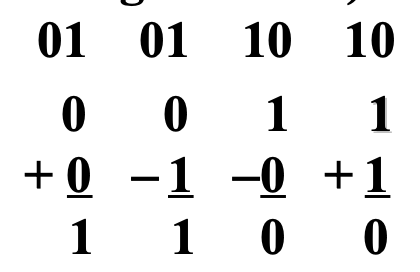
（注：减负数相当于加正数，\(C_{n-1}\) 为 0；加负数相当于减正数，\(C_{n-1}\) 为 1）

得到溢出判断公式：\(V = C_{n-1} \oplus C_{n}\)，这里 \(C_{n}\) 为结果的符号位。

Other Arithmetic Functions¶

Incrementer
- Adding a fixed value to an arithmetic variable
- fixec value = 1, called counting up
- Functional block is called an incrementer
Decrementer
- Subtracting a fixed value from an arithmetic variable
- fixec value = 1, called counting down
- Functional block is called a decrementer
Multiplier by a Constant: shift left
Divider by a Constant: shift right
Zero Fill and Extension
- Zero fill: add 0s to the MSB or LSB
- Extension: add 0s or 1s to the MSB to extend the length of the variable (usually copy the sign bit)

A + 1 Incrementer

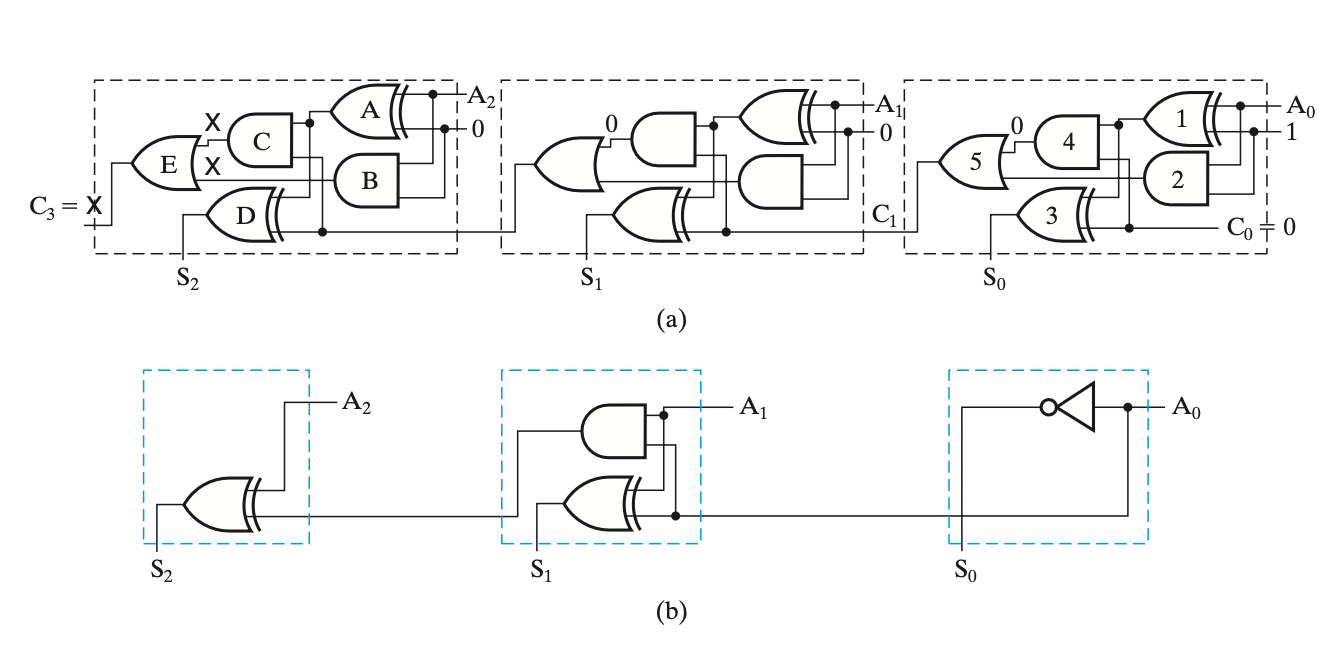
Arithmetic Logic Unit (ALU)¶

Decompose the arithmetic circuit into:

An n-bit parallel adder
A block of logic that selects four choices for the B input of the adder