线代知识回顾¶

Vectors¶

一般记作 \(\vec{a}\) 或者 \(\mathbf{a}\)。

Normalization¶

记作 \(\lVert \vec{a} \rVert\)。

Unit vector: \(\hat{a} = \vec{a} / \lVert \vec{a} \rVert\)。

Dot Product¶

\(\vec{a} \cdot \vec{b} = \lVert \vec{a} \rVert \lVert \vec{b} \rVert \cos \langle \vec{a}, \vec{b} \rangle\)。

\(\cos \langle \vec{a}, \vec{b} \rangle = \frac{\vec{a} \cdot \vec{b}}{\lVert \vec{a} \rVert \lVert \vec{b} \rVert}\)。

对于单位向量，\(\cos \langle \vec{a}, \vec{b} \rangle = \vec{a} \cdot \vec{b}\)。

Projection¶

将 \(\vec{b}\) 投影到 \(\vec{a}\) 上：

\[ \vec{b}_{\bot} = k \hat{a} = \lVert \vec{b} \rVert \cos \langle \vec{a}, \vec{b} \rangle \hat{a} \]

Matrices¶

Identity Matrix and Inverses¶

\(A A^{-1} = A^{-1} A = I\)

\((A B)^{-1} = B^{-1} A^{-1}\)

Transformations¶

实质是对每个点的坐标进行变换。

\(x' = Ax\)

Scaling¶

\[ A = \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} \]

Reflection¶

沿 y 轴反射：

\[ A = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \]

Shear¶

\[ A = \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} \]

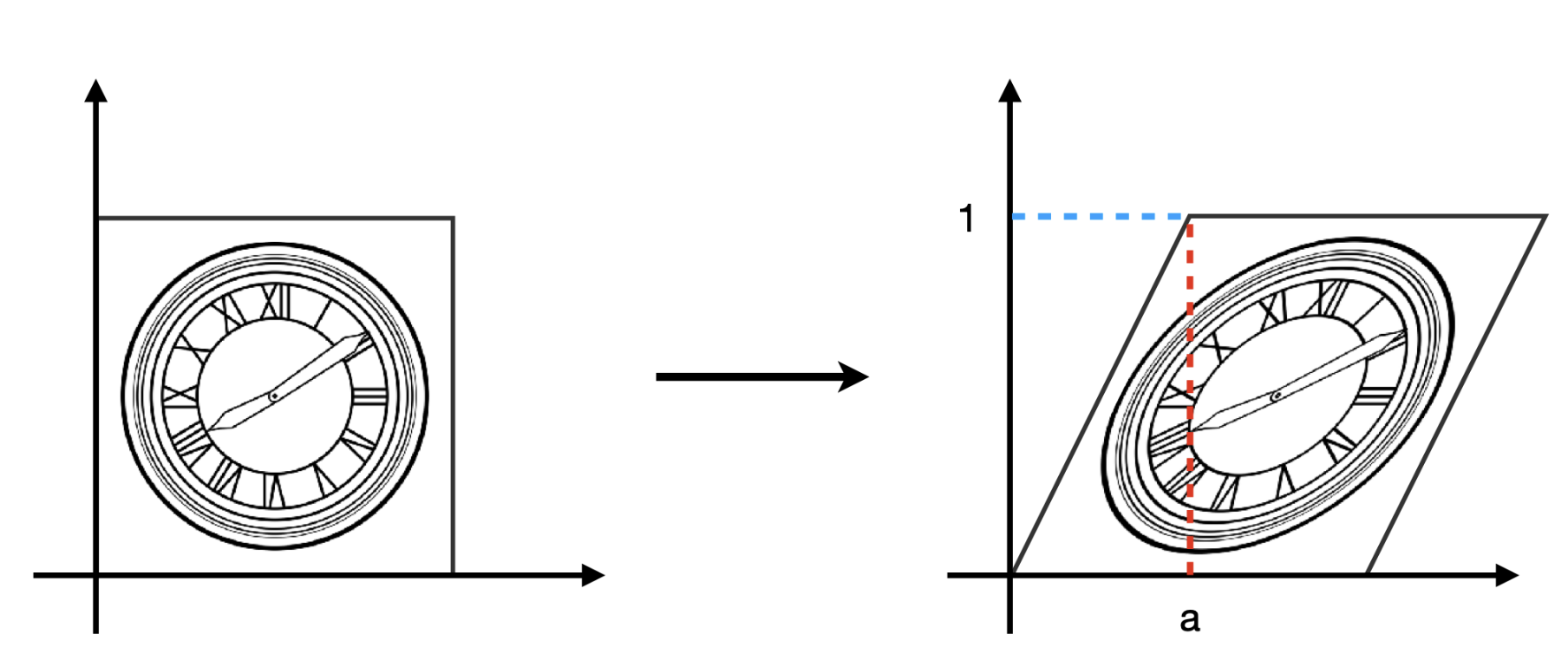
Rotation¶

以原点为中心逆时针旋转 \(\theta\)：

\[ A = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \]

Linear Transforms¶

\[ M = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \]

\(\vec{v'} = M \vec{v}\)

Translation¶

平移不是线性变换。

\[ \begin{aligned} x' &= x + t_x \\ y' &= y + t_y \end{aligned} \]

\[ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} t_x \\ t_y \end{pmatrix} \]

Affine Transforms¶

仿射变换是线性变换和平移的组合。

\[ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} t_x \\ t_y \end{pmatrix} \]

Homogeneous Coordinates¶

齐次坐标，将 2D 坐标转换为 3D 坐标。

\[ \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{bmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \]

Inverse Transform¶

将变换后的坐标转换回原坐标，其代表的变换矩阵为原变换矩阵的逆矩阵。

\[ \begin{aligned} \vec{v'} &= M \vec{v} \\ \vec{v} &= M^{-1} \vec{v'} \end{aligned} \]

Matrix Determinants¶

3 维空间中，三个向量组成的平行六面体的体积，为三个向量组成的行列式的绝对值。

Eigenvectors and Eigenvalues¶

特征值和特征向量。

\[ A \vec{v} = \lambda \vec{v} \]

\(\lambda\) 为特征值，\(\vec{v}\) 为特征向量。

Eigen Decomposition¶

\[ A = Q \Lambda Q^{-1} \]

其中，\(Q\) 为特征向量矩阵，\(\Lambda\) 为特征值矩阵。

PCA (Principal Component Analysis)¶

主成分分析，是一种降维技术。寻找特征空间中的方向，使得数据在这些方向上的投影方差最大。

先将数据中心化，即将横纵坐标减去均值。

\[ A = \begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \\ \vdots & \vdots \\ x_n & y_n \end{bmatrix} \]

矩阵 \(A^T A\) 有两个特征向量，对应两个特征值。

其中较大的特征值对应的特征向量即为主成分，特征值为此方向上的方差。