Relational Model¶

A relational database is a collection of one or more relations, which are based on the relational model.

Example

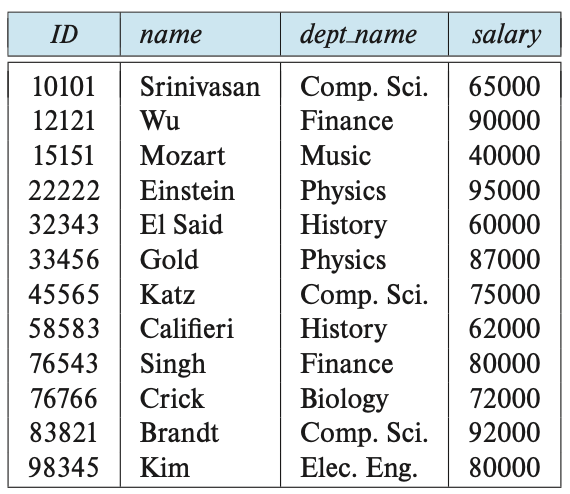
Structure of Relational Databases¶

Basic Structure¶

设集合 \( D_1, D_2, \ldots, D_n \)，关系 \(r\) 是笛卡尔积 \(D_1 \times D_2 \times \ldots \times D_n\) 的一个子集。

Attribute Types¶

设关系 \(r\) 为元组 \( (a_1, a_2, \ldots, a_n) \)，其中 \(a_i\) 是属性，\(D_i\) 是属性的域。每个属性都有名称。

关系理论第一范式

Attribute values are (normally) required to be atomic. 属性值是原子的，即无法分割。例如复合属性或者多值属性都不能成为关系的属性。

\( \mathsf{null} \) 属于每个域。

Concepts about Relation¶

A relation is concerned with two concepts: relation schema and relation instance. 关系包含两个概念：关系模式和关系实例。

Relation Schema: describes the structure of the relation.

Example

Student_schema = (sid: string, name: string, sex: string, age: int, dept: string)

or

Student_schema = (sid, name, sex, age, dept)

Relation Instance: corresponds to the snapshot of the data in the relation at a given instant in time.

The Properties of Relation¶

The order of tuples is irrelevant. 无序
No duplicated tuples in a relation. 无重复
Attribute values are atomic. 属性是原子的

Database¶

A database consists of a collection of relations.

Key¶

\(K \subseteq R\)

Superkey: \(K\) is a superkey of \(R\) if the values of \(K\) are sufficient to identify a unique tuple in \(R\). \(K\) 是 \(R\) 的超键，如果 \(K\) 的值足以唯一标识 \(R\) 中的一个元组。
Candidate Key: \(K\) is a candidate key of \(R\) if \(K\) is a minimal superkey of \(R\). \(K\) 是 \(R\) 的候选键，如果 \(K\) 是 \(R\) 的最小超键。
Primary Key: A candidate key defined by the database designer. 主键是数据库设计者定义的候选键，通常用下划线标识。

Foreign Key¶

Assume relations \(r\) and \(s\): \(r(\underline{A}, B, C)\), \(s(\underline{B}, D)\). \(B\) in relation \(r\) is a foreign key referencing \(s\), and \(r\) is a referencing relation, and \(s\) is a referenced relation.

参照关系中外码的值必须在被参照关系中实际存在, 或为 \( \mathsf{null} \)。

Query Language¶

Pure languages:

Relational Algebra: a procedural query language. 过程式查询语言，SQL 的基础。
Tuple Relational Calculus: 元组关系演算
Domain Relational Calculus: 域关系演算

Fundamental Relational-Algebra Operations¶

Six basic operators:

Selection: \( \sigma \) 选择
Projection: \( \Pi \) 投影
Union: \( \cup \) 并
Set Difference: \( - \) 差
Cartesian product: \( \times \) 笛卡尔积
Rename: \( \rho \) 重命名

Selection¶

\( \sigma_{p} (r) = \{ t \mid t \in r \land p(t) \} \)

\( r \) is a relation
\( p \) is a predicate in the form of <attribute> op <attribute> or <constant>, where op is a comparison operator.

Example

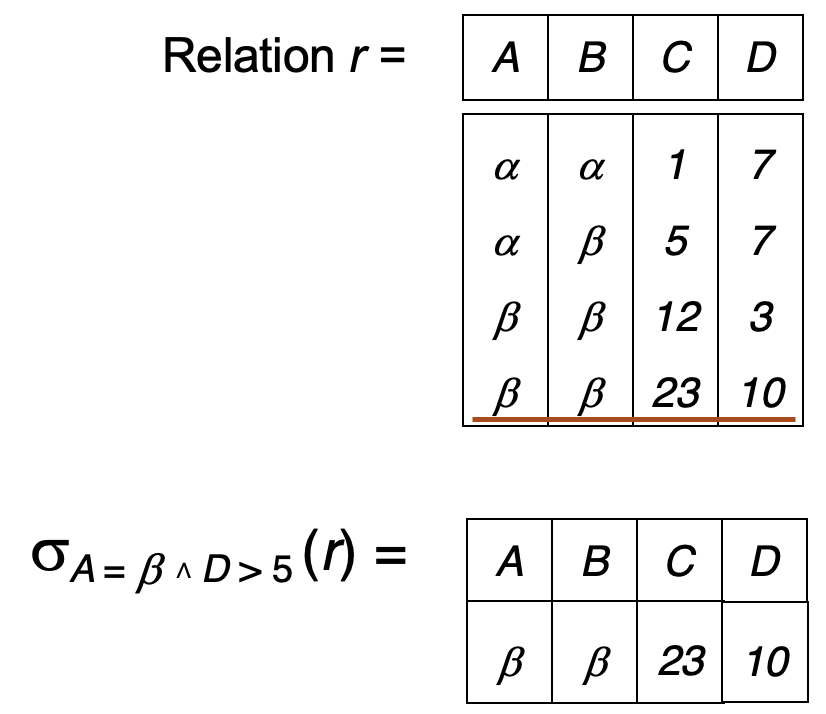
Projection¶

\( \Pi_{A_1, A_2, \ldots, A_k} (r) \)

\( r \) is a relation
\( A_i \) is an attribute of \( r \)

The result is defined as the relation of \(k\) columns obtained by erasing the columns that are not listed. 结果是通过删除未列出的列而获得的 \(k\) 列关系。并且进行去重。

Example

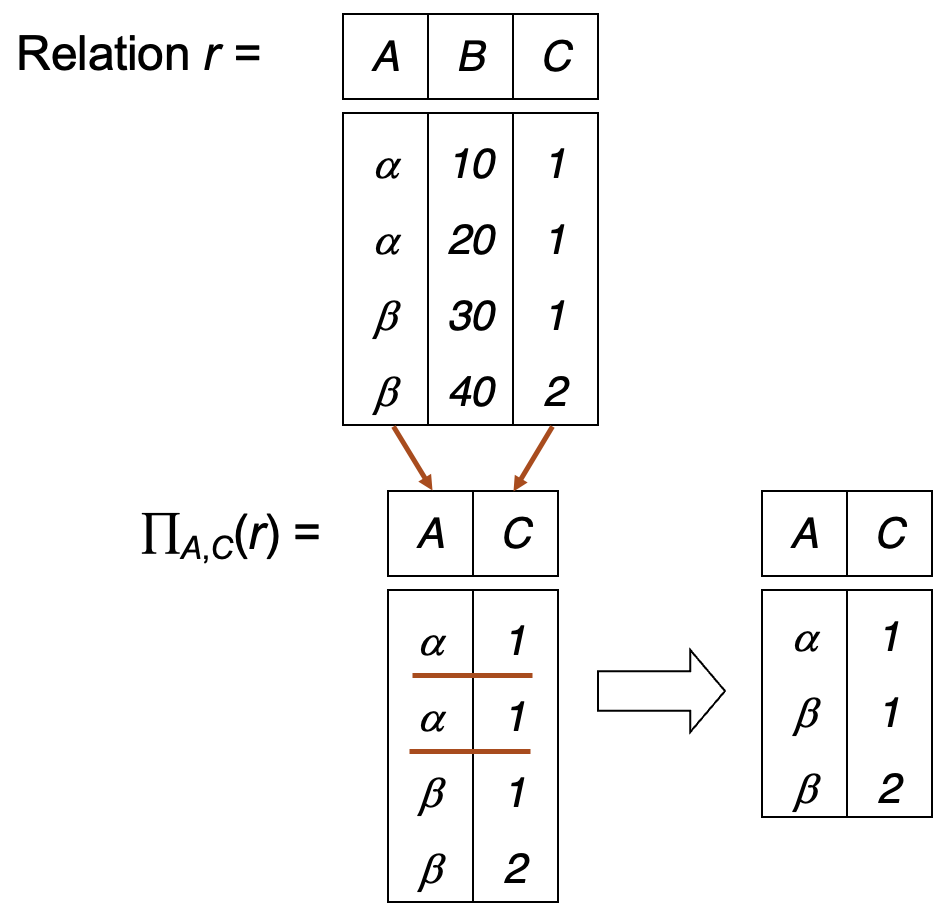
Union¶

\( r \cup s = \{ t \mid t \in r \lor t \in s \} \)

\( r \) and \( s \) are relations
\( r \) and \( s \) must have the same number of attributes. \( r \) 和 \( s \) 必须有相同数量的属性。
The attribute domains must be compatible. 属性域必须兼容。

Example

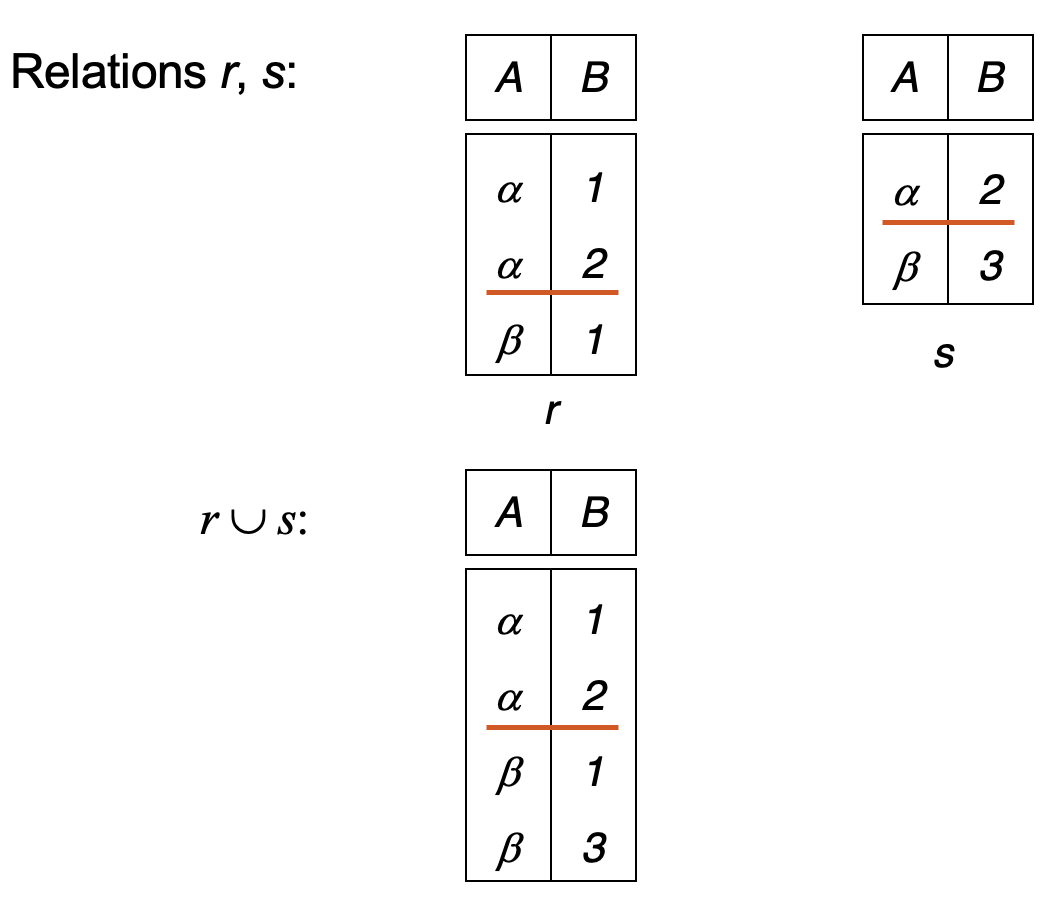
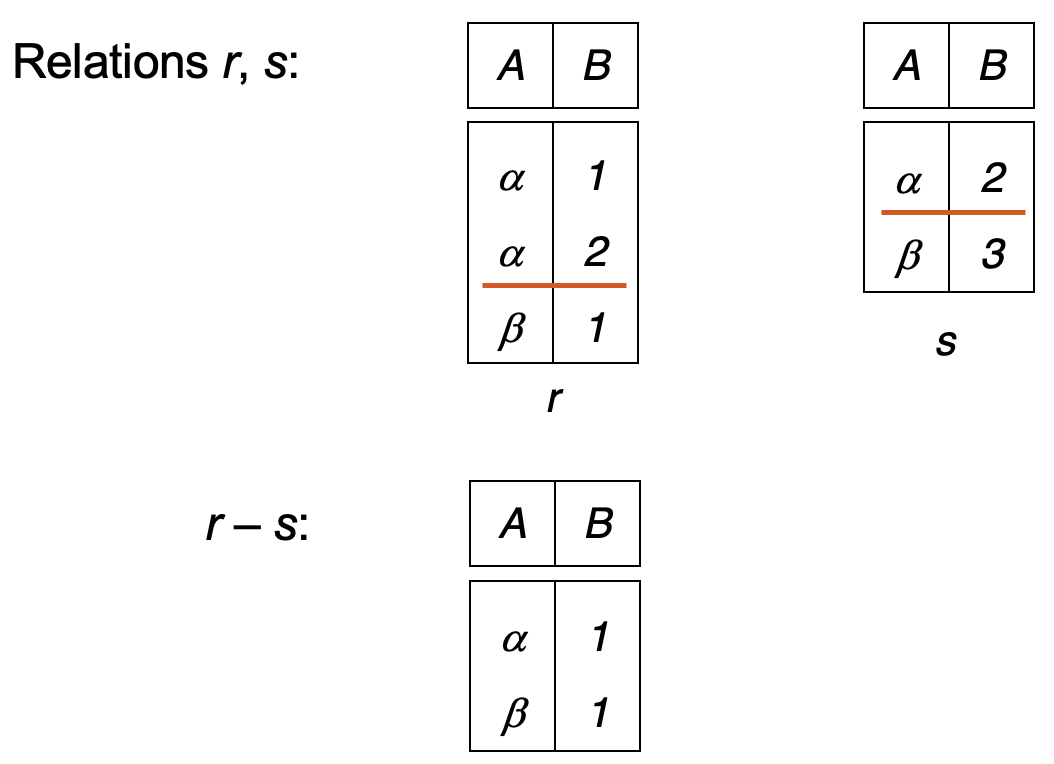
Set Difference¶

\( r - s = \{ t \mid t \in r \land t \notin s \} \)

\( r \) and \( s \) are relations
Similar to Union, \( r \) and \( s \) must have the same number of attributes and the attribute domains must be compatible.

Example

Cartesian Product¶

\( r \times s = \{ (t_1, t_2) \mid t_1 \in r \land t_2 \in s \} \)

\( r \) and \( s \) are relations
If \( r \) and \( s \) are not disjoint, then rename will be used to avoid ambiguity between the attributes with the same name. 如果 \( r \) 和 \( s \) 有相同名称的属性，则将使用 重命名 来避免具有相同名称的属性之间的歧义。

Example

\( r \) 和 \( s \) 不相交：

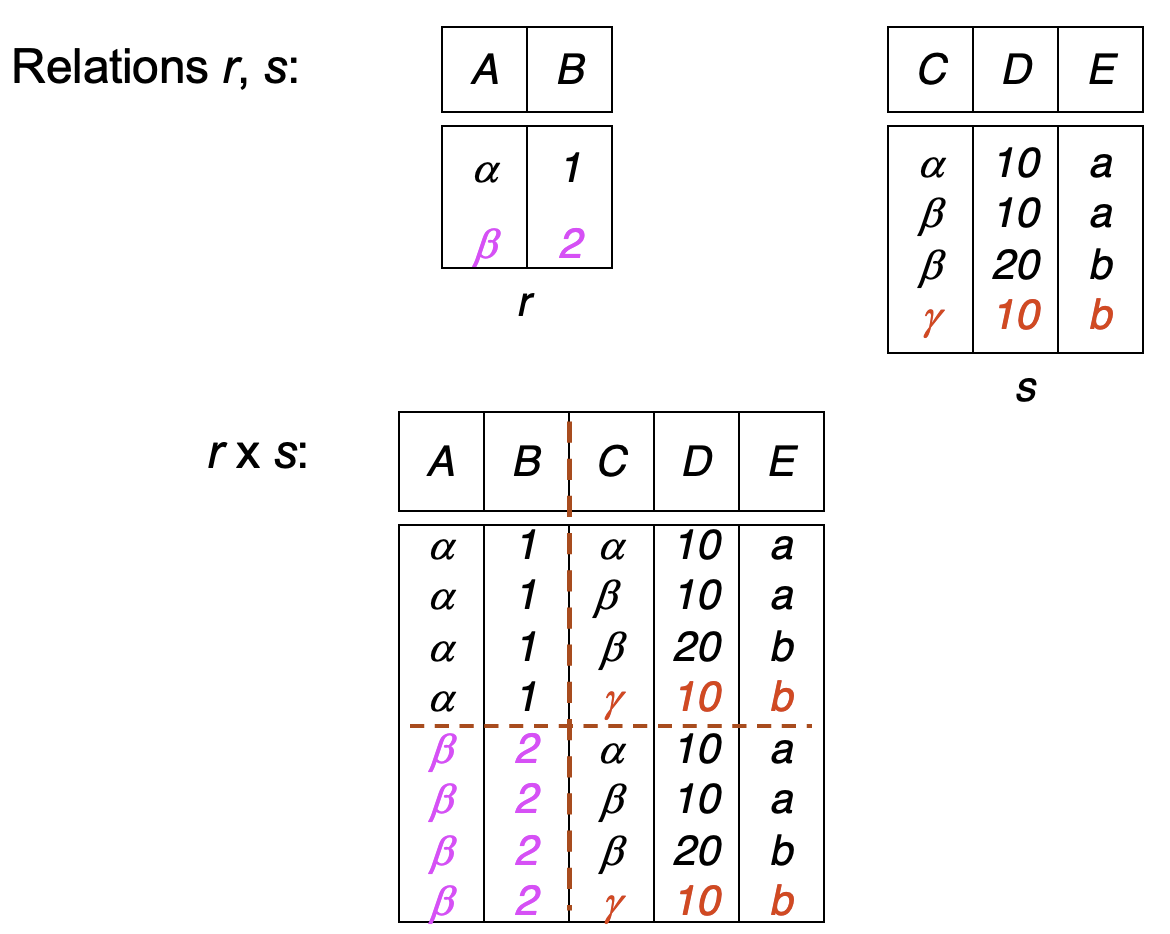
\( r \) 和 \( s \) 相交：

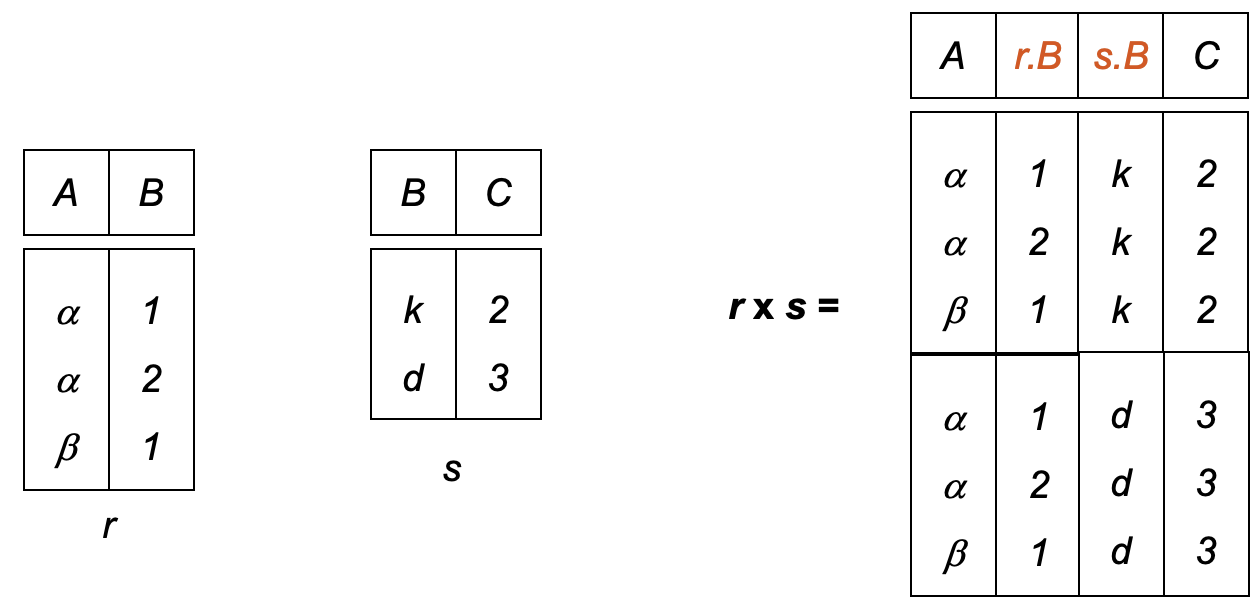
Rename¶

\( \rho_X (E) \): rename the expression \(E\) as \(X\).
\( \rho_{X(A_1, A_2, \ldots, A_n)} (E) \): rename the expression \(E\) as \(X\) and the attributes as \(A_1, A_2, \ldots, A_n\).

\( \rho \) returns a relation that is identical to \(E\) except that the relation is renamed as \(X\). \( \rho \) 返回一个与 \(E\) 相同的关系，只是关系被重命名为 \(X\)。

Additional Relational-Algebra Operations¶

Four additional operators:

Set Intersection: \( \cap \) 交
Natural Join: \( \bowtie \) 自然连接
Division: \( \div \) 除
Assignment: \( \leftarrow \) 赋值

Set Intersection¶

\( r \cap s = \{ t \mid t \in r \land t \in s \} = r - (r - s) \)

\( r \) and \( s \) are relations
\( r \) and \( s \) must have the same number of attributes and the attribute domains must be compatible.

Example

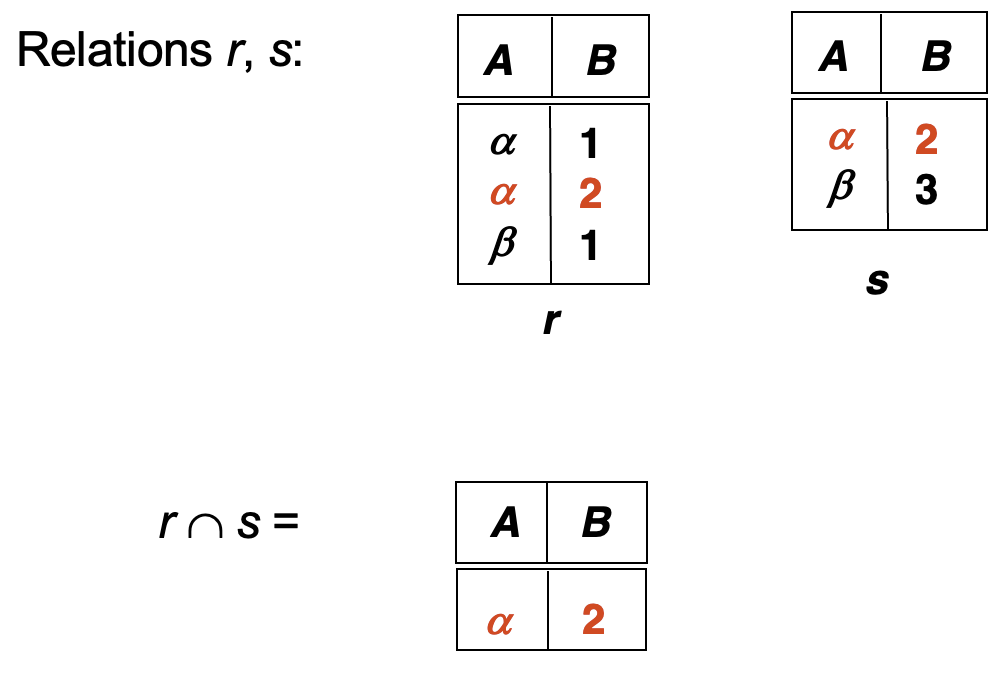
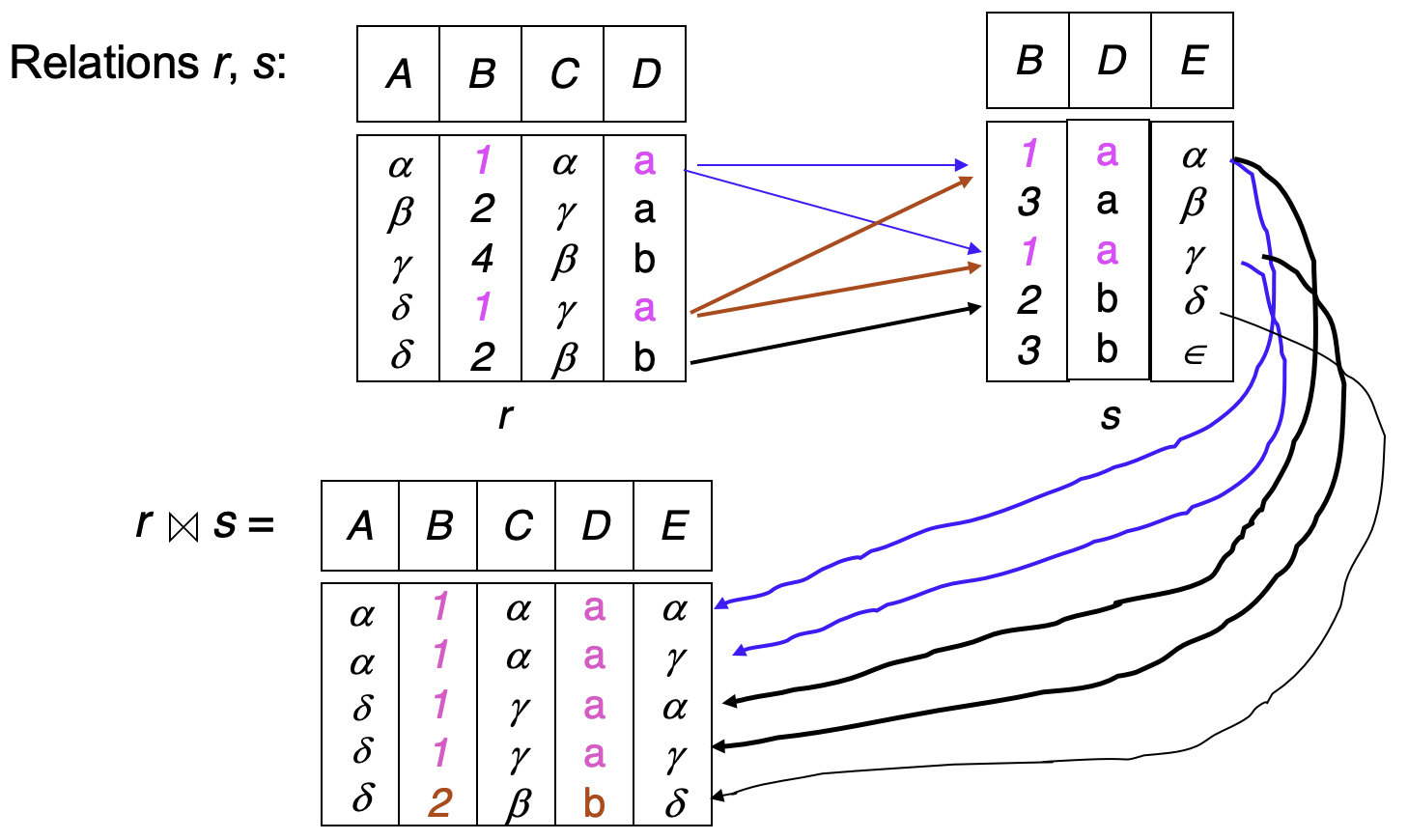
Natural Join¶

\( r \bowtie s \)

\( r \) and \( s \) are relations
Consider each pair of tuples \( t_1 \in r \) and \( t_2 \in s \), if \( t_1 \) and \( t_2 \) have the same value on each attribute in \( R \cap S \), then add a tuple to the result relation with the remaining attributes from \( t_1 \) and \( t_2 \). 如果 \( t_1 \) 和 \( t_2 \) 在 \( R \cap S \) 上的每个属性上具有相同的值，则将一个元组添加到结果关系中，该元组具有来自 \( t_1 \) 和 \( t_2 \) 的剩余属性。

Example

Theta Join Operation

\( r \bowtie_{\theta} s = \sigma_{\theta} (r \times s) \)

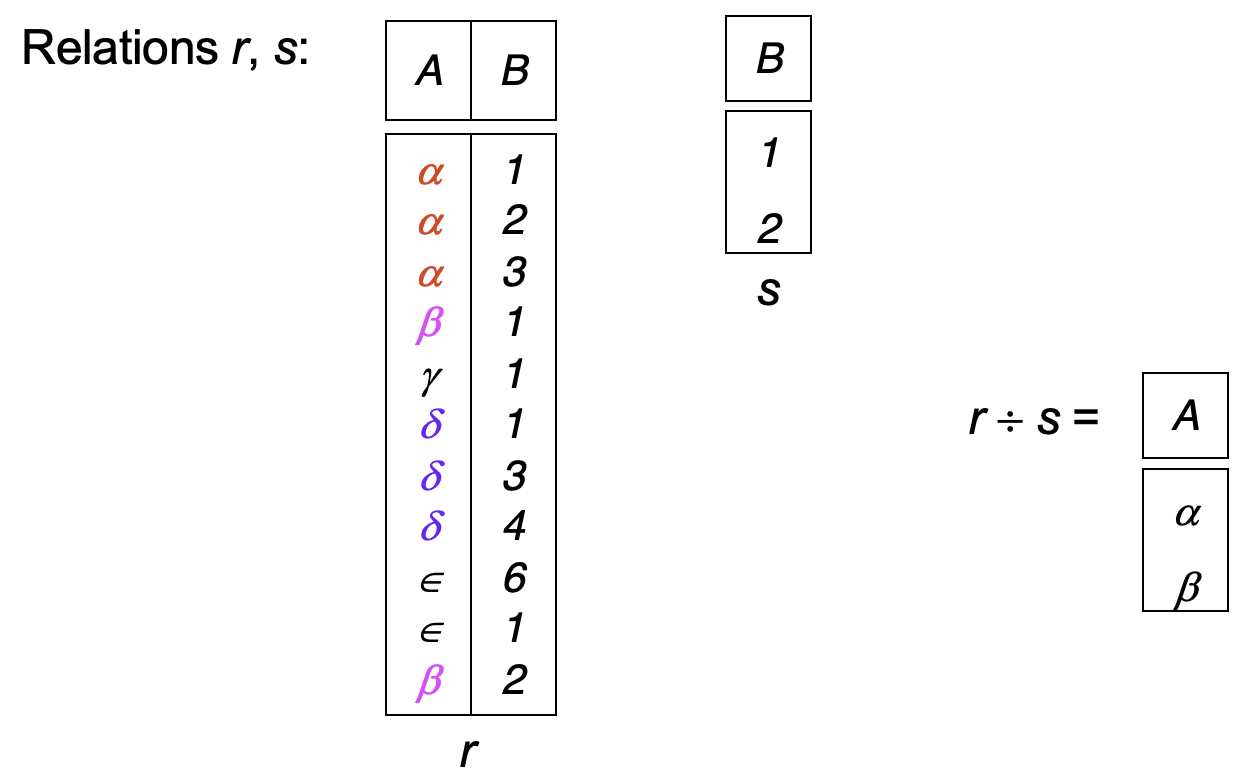
Division¶

\( r \div s = \{ t \mid t \in \Pi_{R - S} (r) \land \forall u \in s, t \times u \in r \} \)

\( r \) and \( s \) are relations on schema \( R and S \)

Example

Assignment¶

\( X \leftarrow E \)

Assignment is always made to a temporary relation.

Example

Write \( r \div s \) as:

\[ \begin{align*} temp1 &\leftarrow \Pi_{R - S} (r) \\ temp2 &\leftarrow \Pi_{R - S} (temp1 \times s - \Pi_{R - S, S} (r)) \\ result &\leftarrow temp1 - temp2 \end{align*} \]

Extended Relational-Algebra Operations¶

Generalized Projection: \( \Pi_{A_1, A_2, \ldots, A_n} (r) \) where \( A_i \) is an expression. 广义投影
Aggregation Functions: 聚合函数

Generalized Projection¶

\( \Pi_{A_1, A_2, \ldots, A_n} (r) \) where \( A_i \) is an expression.

Example

Given a relation \( \text{credit_info}(\text{customer_name}, \text{limit}, \text{current_balance}) \), we can use the following expression to calculate the available credit for each customer:

\[ \Pi_{\text{customer_name}, \text{limit} - \text{current_balance}} (\text{credit_info}) \]

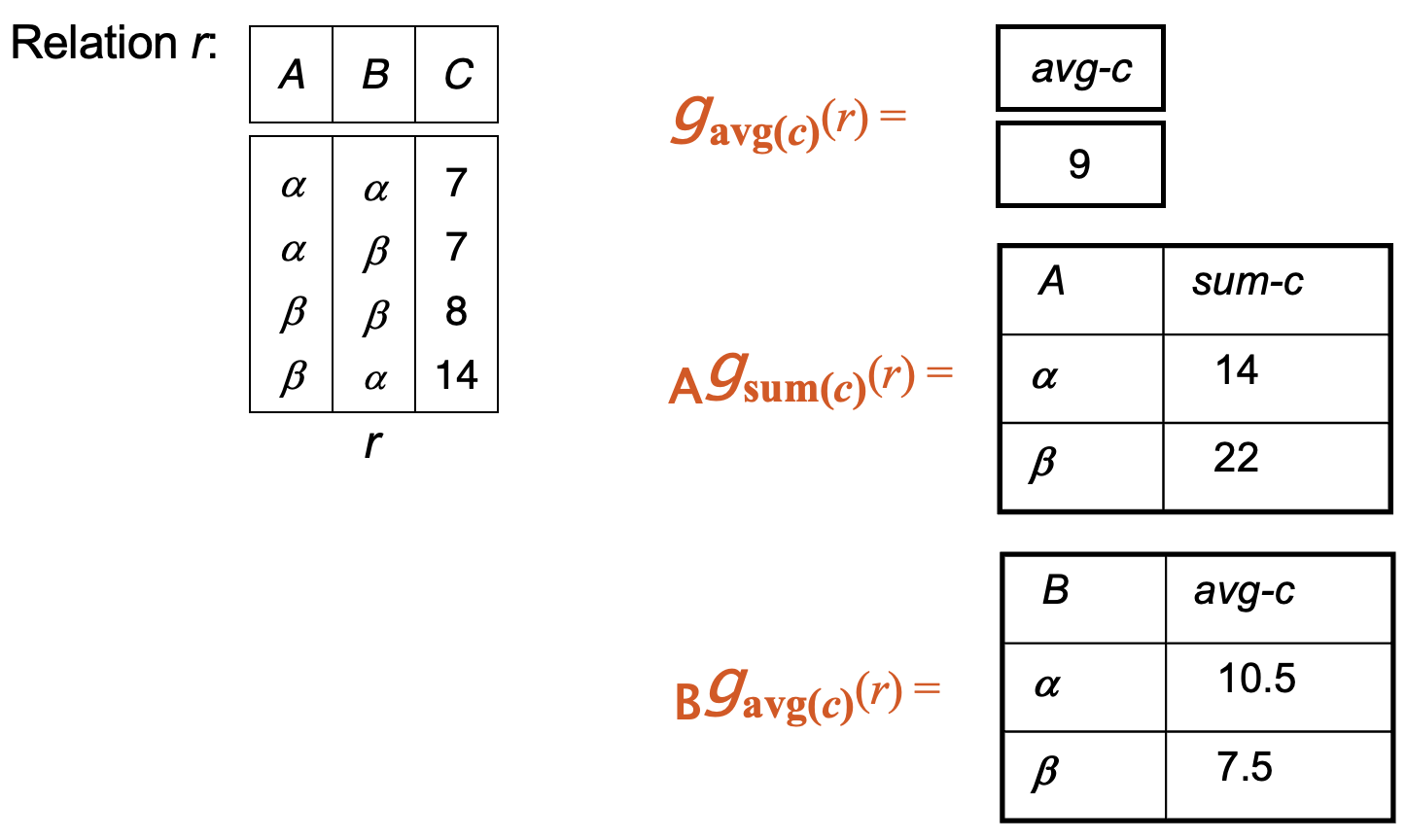
Aggregation Functions¶

\( _{G_1, G_2, \ldots, G_n}g_{F_1(A_1), F_2(A_2), \ldots, F_n(A_n)} (r) \)

\( r \) is a relation
\( A_i \) is an attribute of \( r \)
\( F_i \) is an aggregation function, such as
- avg: average value
- sum: sum of values
- count: number of tuples
- max: maximum value
- min: minimum value
\( G_i \) is a grouping attribute(can be empty)

Example

Info

Result of aggregation does not have a name. 聚合的结果没有名称，需要重命名或者在聚合操作中指定名称。

Example:

\[ _\text{branch-name} g_{\text{sum}(\text{balance}) \ as \ \text{sum-balance}} (\text{account}) \]

Modification of the Database¶

Deletion
Insertion
Updating

Deletion¶

\( r \leftarrow r - E \)

\( r \) is a relation
\( E \) is a relational-algebra expression

Insertion¶

\( r \leftarrow r \cup E \)

Updating¶

\( r \leftarrow \Pi_{F_1, F_2, \ldots, F_n} (r) \)

\( r \) is a relation
\( F_i \) is an attribute of \( r \) or an expression which gives the new value of the attribute