量子比特与量子门¶

术语对照¶

量子术语	线代术语
态矢量（State Vector）	向量（Vector）
本征态（Eigenstate）	特征向量（Eigenvector）
本征值（Eigenvalue）	特征值（Eigenvalue）
右矢（Ket）\( \left\lvert a \right\rangle \)	列向量
左矢（Bra）\( \left\langle a \right\rvert \)	行向量
\( \left\langle a \vert b \right\rangle \)	向量内积
\( \left\lvert a \right\rangle \left\langle b \right\rvert \)	向量外积
基态（Ground State）	最小本征态（Eigenstate with the smallest Eigenvalue）
算符（Operator）	矩阵（Matrix）
线性算符（Linear Operator）	线性变换（Linear Transformation）
幺正（酉）算符（Unitary Operator）\(HH^{\dagger} = I\)	正交矩阵（Orthogonal Matrix）
厄米矩阵（Hermitian Matrix）\(H = H^{\dagger}\)	自伴随矩阵（Self-adjoint Matrix）
线性叠加原理（Superposition Principle）	线性组合性质（Linearity）
投影算符（Projection Operator）	投影矩阵（Projection Matrix）

单量子比特¶

DiVincenzo 判据¶

判断一个物理系统是否适合用于量子计算的五个条件：

具有可控的量子比特，并具有可扩充性（可调控的二能级系统）
能够初始化量子比特为 \( \left\lvert 0 \right\rangle \) 态或 \( \left\lvert 1 \right\rangle \) 态
具有长相关退相干时间，确保有充足的时间进行量子操作
有一个通用的量子门集合，能够对量子比特进行任意幺正操作
能够测量量子比特的状态

量子态¶

量子叠加态：量子比特可以表示为基态的线性组合。
量子纠缠：一对量子比特对的两个量子比特存在于单个量子状态，当以可预测的方式改变其中一个量子比特的状态时，另一个量子比特的状态将改变。

基矢态¶

任意两个单位正交基都可以作为量子态的基矢态。

常用的有：

\( \left\lvert 0 \right\rangle \) 和 \( \left\lvert 1 \right\rangle \)
\( \left\lvert + \right\rangle \) 和 \( \left\lvert - \right\rangle \)

\[ \begin{aligned} \left\lvert + \right\rangle & = \frac{1}{\sqrt{2}} \left( \left\lvert 0 \right\rangle + \left\lvert 1 \right\rangle \right) \\ \left\lvert - \right\rangle & = \frac{1}{\sqrt{2}} \left( \left\lvert 0 \right\rangle - \left\lvert 1 \right\rangle \right) \end{aligned} \]

任意量子态 \( \left\lvert \varphi \right\rangle \) 可以表示为基矢态的线性组合：

\[ \left\lvert \varphi \right\rangle = \alpha \left\lvert 0 \right\rangle + \beta \left\lvert 1 \right\rangle \]

其中 \( \alpha \) 和 \( \beta \) 是复系数（振幅），满足 \( \left| \alpha \right|^2 + \left| \beta \right|^2 = 1 \)。

量子态矢内积¶

bra-ket 表示法：bra 表示行向量，ket 表示列向量。

\( \left\langle \varphi \right\lvert = \left( \alpha^*, \beta^* \right) \) 是 \( \left\lvert \varphi \right\rangle = \begin{bmatrix} \alpha \\ \beta \end{bmatrix} \) 的共轭转置。

内积定义：

\[ \left\langle a \vert b \right\rangle = a_1^* b_1 + a_2^* b_2 + \cdots + a_n^* b_n \]

若两向量内积为 0，则两向量正交。

定义量子态的欧几里得范数为 \( \left\lVert \left\lvert \varphi \right\rangle \right\rVert = \sqrt{\left\langle \varphi \vert \varphi \right\rangle} \)。

量子态的坍缩¶

当对量子态进行测量时，量子态会坍缩到测量结果对应的本征态上。

测量 \( \left\lvert \varphi \right\rangle = \alpha \left\lvert 0 \right\rangle + \beta \left\lvert 1 \right\rangle \)，有概率 \( \left| \alpha \right|^2 \) 得到 \( \left\lvert 0 \right\rangle \)，概率 \( \left| \beta \right|^2 \) 得到 \( \left\lvert 1 \right\rangle \)。

归一化条件：\( \left| \alpha \right|^2 + \left| \beta \right|^2 = 1 \)。

不可克隆原理

量子态的坍缩导致量子态的不可克隆，即不可能复制一个未知的量子态。

不存在一个线性算符 \( U \) 能够将 \( \left\lvert \varphi \right\rangle \left\lvert 0 \right\rangle \) 映射到 \( \left\lvert \varphi \right\rangle \left\lvert \varphi \right\rangle \)。

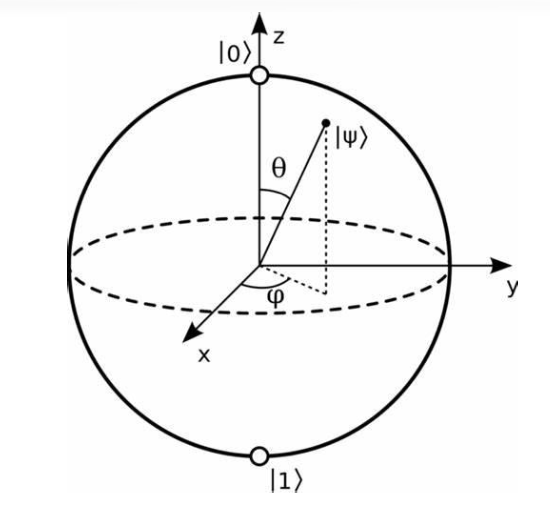
量子比特的几何表示¶

可以将单量子比特的量子态可视化在一个球面中，这个球面称为 Bloch 球。

将量子态写成 \( \left\lvert \varphi \right\rangle = \cos \frac{\theta}{2} \left\lvert 0 \right\rangle + e^{i \phi} \sin \frac{\theta}{2} \left\lvert 1 \right\rangle \)，其中 \( \theta \) 和 \( \phi \) 是极角，可以表示在球面上的点。

Bloch 球只能可视化单个量子比特的状态。

多量子比特¶

多量子比特的表示¶

n 量子比特可以表示为 \( 2^n \) 维复向量空间中的一个向量。以两量子比特为例：

\[ \left\lvert \varphi \right\rangle = \alpha_{00} \left\lvert 00 \right\rangle + \alpha_{01} \left\lvert 01 \right\rangle + \alpha_{10} \left\lvert 10 \right\rangle + \alpha_{11} \left\lvert 11 \right\rangle \]

其中 \( \alpha_{ij} \) 是复系数，满足归一化条件。

如果进行测量，两量子比特的状态会坍缩到测量结果对应的本征态上。

如果仅测量低位量子比特，则有 \( \left\lvert \alpha_{00} \right\rvert^2 + \left\lvert \alpha_{01} \right\rvert^2 \) 的概率得到 \( \left\lvert 0 \right\rangle \)，测量之后量子态坍缩为

\[ \left\lvert \varphi \right\rangle = \frac{\alpha_{00} \left\lvert 00 \right\rangle + \alpha_{01} \left\lvert 01 \right\rangle}{\sqrt{\left\lvert \alpha_{00} \right\rvert^2 + \left\lvert \alpha_{01} \right\rvert^2}} \]

张量积¶

又称 Kronecker 积，将两个向量空间的向量合并成一个更大的向量空间，算符为 \( \otimes \)。

判断是否纠缠¶

两量子比特的态矢量为

\[ \left\lvert \varphi \right\rangle = \alpha_{00} \left\lvert 00 \right\rangle + \alpha_{01} \left\lvert 01 \right\rangle + \alpha_{10} \left\lvert 10 \right\rangle + \alpha_{11} \left\lvert 11 \right\rangle \]

若两个量子比特无关，则不纠缠。例：

\( \left\lvert \varphi \right\rangle = \alpha_{00} \left\lvert 00 \right\rangle + \alpha_{11} \left\lvert 11 \right\rangle \) 为纠缠态，测量一个量子比特的状态会影响另一个量子比特的状态。
\( \left\lvert \varphi \right\rangle = \alpha \left\lvert 00 \right\rangle + \alpha \left\lvert 01 \right\rangle = \alpha \left\lvert 0 \right\rangle \left( \left\lvert 0 \right\rangle + \left\lvert 1 \right\rangle \right) \) 为非纠缠态。

贝尔态¶

贝尔态是两量子比特的纠缠态之一，有四种形式：

\[ \begin{aligned} \left\lvert \phi^+ \right\rangle & = \frac{1}{\sqrt{2}} \left( \left\lvert 00 \right\rangle + \left\lvert 11 \right\rangle \right) \\ \left\lvert \phi^- \right\rangle & = \frac{1}{\sqrt{2}} \left( \left\lvert 00 \right\rangle - \left\lvert 11 \right\rangle \right) \\ \left\lvert \psi^+ \right\rangle & = \frac{1}{\sqrt{2}} \left( \left\lvert 01 \right\rangle + \left\lvert 10 \right\rangle \right) \\ \left\lvert \psi^- \right\rangle & = \frac{1}{\sqrt{2}} \left( \left\lvert 01 \right\rangle - \left\lvert 10 \right\rangle \right) \end{aligned} \]

\(\{ \left\lvert \phi^+ \right\rangle, \left\lvert \phi^- \right\rangle, \left\lvert \psi^+ \right\rangle, \left\lvert \psi^- \right\rangle \}\) 称为贝尔基。

单量子比特门¶

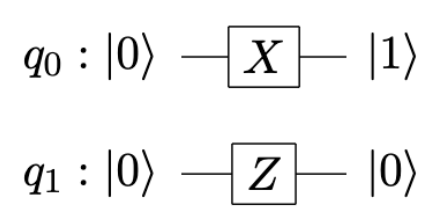
X 门¶

非门，作用为 \( X \left\lvert 0 \right\rangle = \left\lvert 1 \right\rangle \) 和 \( X \left\lvert 1 \right\rangle = \left\lvert 0 \right\rangle \)。

对应矩阵为

\[ X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \]

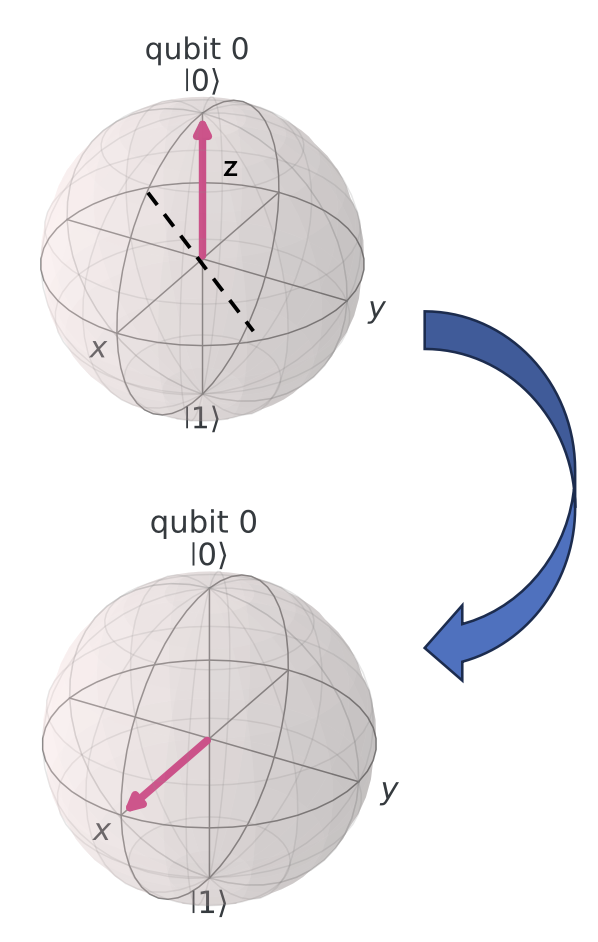
Hadamard 门¶

可以将基态 \( \left\lvert 0 \right\rangle \) 和 \( \left\lvert 1 \right\rangle \) 均匀地映射到 \( \left\lvert + \right\rangle \) 和 \( \left\lvert - \right\rangle \)，生成叠加态。

作用为

\[ \begin{aligned} H \left\lvert 0 \right\rangle & = \frac{1}{\sqrt{2}} \left( \left\lvert 0 \right\rangle + \left\lvert 1 \right\rangle \right) = \left\lvert + \right\rangle \\ H \left\lvert 1 \right\rangle & = \frac{1}{\sqrt{2}} \left( \left\lvert 0 \right\rangle - \left\lvert 1 \right\rangle \right) = \left\lvert - \right\rangle \end{aligned} \]

对应矩阵为

\[ H = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \]

H 门的实质

H 门实际上是实现将量子态从 z 基到 x 基的转变。

泡利门¶

Pauli 门包括 X 门、Y 门和 Z 门。

\[ \begin{aligned} \sigma_x & = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \\ \sigma_y & = \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix} \\ \sigma_z & = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \end{aligned} \]

分别对应于 Bloch 球上绕 x、y 和 z 轴旋转 \( \pi \)。

量子门与矩阵乘法

量子门实质上是酉矩阵，满足 \( UU^{\dagger} = I \)，满足可逆和正则性。

厄米矩阵 \( H = H^{\dagger} \)，保证其本征值为实数且本征向量正交，确保了量子系统的物理量是可观测的。
酉矩阵 \( UU^{\dagger} = I \)，保持内积不变，保证了量子态的归一性，保持态矢量之间的正交性质。

相位旋转门¶

相位旋转门作用于量子比特的态矢量时，会引入一个特定的相位因子，改变量子态的相对相位；具体而言，相位的旋转是通过调整量子比特的状态矢量与某个特定基态的相对相位来实现的。相位旋转门可以改变量子态的相对相位，但不改变其概率分布。

常见的相位旋转门有 P 门、T 门、S 门。

\[ \begin{aligned} P(\theta) & = \begin{bmatrix} 1 & 0 \\ 0 & e^{i \theta} \end{bmatrix} \\ T & = \begin{bmatrix} 1 & 0 \\ 0 & e^{i \frac{\pi}{4}} \end{bmatrix} \\ S & = \begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix} \end{aligned} \]

参数旋转门¶

分别绕 x、y、z 轴旋转角度 \( \theta \) 的旋转门：

\[ \begin{aligned} R_x(\theta) & = \begin{bmatrix} \cos \frac{\theta}{2} & -i \sin \frac{\theta}{2} \\ -i \sin \frac{\theta}{2} & \cos \frac{\theta}{2} \end{bmatrix} \\ R_y(\theta) & = \begin{bmatrix} \cos \frac{\theta}{2} & -\sin \frac{\theta}{2} \\ \sin \frac{\theta}{2} & \cos \frac{\theta}{2} \end{bmatrix} \\ R_z(\theta) & = \begin{bmatrix} e^{-i \frac{\theta}{2}} & 0 \\ 0 & e^{i \frac{\theta}{2}} \end{bmatrix} \end{aligned} \]

容易验证 \( H = i R_y(\frac{\pi}{2}) R_z(\pi) = i R_x(\pi) R_y(\frac{\pi}{2}) \)。

单量子比特门操作分解¶

任意酉矩阵都可以分解为：

\[ U = e^{i \alpha} \begin{bmatrix} e^{-i \frac{\beta}{2}} & 0 \\ 0 & e^{i \frac{\beta}{2}} \end{bmatrix} \begin{bmatrix} \cos \frac{\gamma}{2} & -\sin \frac{\gamma}{2} \\ \sin \frac{\gamma}{2} & \cos \frac{\gamma}{2} \end{bmatrix} \begin{bmatrix} e^{-i \frac{\delta}{2}} & 0 \\ 0 & e^{i \frac{\delta}{2}} \end{bmatrix} \]

分解为绕 z 轴旋转 \( \delta \)、绕 y 轴旋转 \( \gamma \)、绕 z 轴旋转 \( \beta \) 和全局相位 \( e^{i \alpha} \)。

多量子门¶

纠缠判定¶

如果一个多量子比特系统可以分解为多个单量子比特的张量积，那么这个系统被称作无关的、可分的；反之，该系统是不可分的、纠缠的。

Example

量子态

\[ \left\lvert \varphi \right\rangle = \frac{1}{2} \left\lvert 00 \right\rangle + \frac{i}{2} \left\lvert 01 \right\rangle - \frac{1}{2} \left\lvert 10 \right\rangle - \frac{i}{2} \left\lvert 11 \right\rangle \]

可以分解为

\[ \left( \frac{1}{\sqrt{2}} \left\lvert 0 \right\rangle - \frac{1}{\sqrt{2}} \left\lvert 1 \right\rangle \right) \otimes \left( \frac{1}{\sqrt{2}} \left\lvert 0 \right\rangle + \frac{i}{\sqrt{2}} \left\lvert 1 \right\rangle \right) \]

说明该量子态是可分的。

复合系统¶

可以将多量子比特系统看作一个整体，称为复合系统。

Example

双量子态系统如下：

若将两个单量子门视作整体，可以通过张量积合成为一个双量子门

\[ X \otimes Z = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \otimes \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} = \begin{bmatrix} 0 \cdot \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} & 1 \cdot \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \\ 1 \cdot \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} & 0 \cdot \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \end{bmatrix} = \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \\ 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \end{bmatrix} \]

作用于复合系统：

\[ X \otimes Z \left\lvert 00 \right\rangle = \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \\ 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} = \left\lvert 10 \right\rangle \]

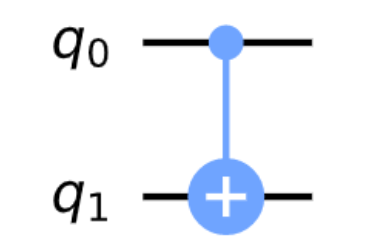
CNOT 门¶

CNOT 门是控制非门，作用于两量子比特系统，当控制量子比特为 \( \left\lvert 1 \right\rangle \) 时，对目标量子比特施加 X 门。

制备纠缠态

\[ \begin{aligned} \left\lvert 0 \right\rangle \left\lvert 0 \right\rangle & \xrightarrow{H \otimes I} \frac{1}{\sqrt{2}} \left( \left\lvert 0 \right\rangle + \left\lvert 1 \right\rangle \right) \left\lvert 0 \right\rangle = \frac{1}{\sqrt{2}} \left( \left\lvert 00 \right\rangle + \left\lvert 10 \right\rangle \right) \\ & \xrightarrow{\text{CNOT gate}} \frac{1}{\sqrt{2}} \left( \left\lvert 00 \right\rangle + \left\lvert 11 \right\rangle \right) \end{aligned} \]

量子隐形传态¶

假设有处于贝尔纠缠态的双量子比特系统

\[ \left\lvert q_0 q_1\right\rangle = \frac{1}{\sqrt{2}} \left( \left\lvert 00 \right\rangle + \left\lvert 11 \right\rangle \right) \]

Alice 拿走了量子比特 \( q_0 \)，Bob 拿走了量子比特 \( q_1 \)。

现在 Alice 想要将一个量子态 \( \left\lvert \psi \right\rangle = \alpha \left\lvert 0 \right\rangle + \beta \left\lvert 1 \right\rangle \) 传输给 Bob。

Alice 和 Bob 持有的三个量子态构成的初始量子系统为

\[ \left\lvert \psi_0 \right\rangle = \frac{1}{\sqrt{2}} \left( \alpha \left\lvert 0 \right\rangle ( \left\lvert 00 \right\rangle + \left\lvert 11 \right\rangle ) + \beta \left\lvert 1 \right\rangle ( \left\lvert 00 \right\rangle + \left\lvert 11 \right\rangle ) \right) \]

Alice 首先对 \( \left\lvert \psi \right\rangle \) 和 \( q_0 \) 进行 CNOT 门操作，其中 \( \left\lvert \psi \right\rangle \) 为控制量子比特，\( q_0 \) 为目标量子比特，量子系统变为

\[ \left\lvert \psi_1 \right\rangle = \frac{1}{\sqrt{2}} \left( \alpha \left\lvert 0 \right\rangle ( \left\lvert 00 \right\rangle + \left\lvert 11 \right\rangle ) + \beta \left\lvert 1 \right\rangle ( \left\lvert 10 \right\rangle + \left\lvert 01 \right\rangle ) \right) \]

然后 Alice 对 \( \left\lvert \psi \right\rangle \) 进行 Hadamard 门操作，量子系统变为

\[ \begin{aligned} \left\lvert \psi_2 \right\rangle &= \frac{1}{2} \left( \alpha ( \left\lvert 0 \right\rangle + \left\lvert 1 \right\rangle ) ( \left\lvert 00 \right\rangle + \left\lvert 11 \right\rangle ) + \beta ( \left\lvert 0 \right\rangle - \left\lvert 1 \right\rangle ) ( \left\lvert 10 \right\rangle + \left\lvert 01 \right\rangle ) \right) \\ &= \frac{1}{2} \left( \left\lvert 00 \right\rangle ( \alpha \left\lvert 0 \right\rangle + \beta \left\lvert 1 \right\rangle ) + \left\lvert 01 \right\rangle ( \alpha \left\lvert 1 \right\rangle + \beta \left\lvert 0 \right\rangle ) + \left\lvert 10 \right\rangle ( \alpha \left\lvert 0 \right\rangle - \beta \left\lvert 1 \right\rangle ) + \left\lvert 11 \right\rangle ( \alpha \left\lvert 1 \right\rangle - \beta \left\lvert 0 \right\rangle ) \right) \end{aligned} \]

此时 Alice 对自己持有的两个量子态进行测量，测量结果可能为 \( \left\lvert 00 \right\rangle \)、\( \left\lvert 01 \right\rangle \)、\( \left\lvert 10 \right\rangle \)、\( \left\lvert 11 \right\rangle \) 中的一个。Alice 将自己的测量结果发送给 Bob，Bob 根据 Alice 的测量结果对自己持有的量子态进行操作，使得 Bob 持有的量子态与 Alice 想要传输的量子态相同。

若 Alice 的测量结果为 \( \left\lvert 00 \right\rangle \)，由于量子纠缠，Bob 持有的量子态为 \( \alpha \left\lvert 0 \right\rangle + \beta \left\lvert 1 \right\rangle \)，即 Alice 想要传输的量子态，不需要任何操作。
若 Alice 的测量结果为 \( \left\lvert 01 \right\rangle \)，Bob 持有的量子态为 \( \alpha \left\lvert 1 \right\rangle + \beta \left\lvert 0 \right\rangle \)，Bob 需要对自己持有的量子态进行 X 门操作。
若 Alice 的测量结果为 \( \left\lvert 10 \right\rangle \)，Bob 持有的量子态为 \( \alpha \left\lvert 0 \right\rangle - \beta \left\lvert 1 \right\rangle \)，Bob 需要对自己持有的量子态进行 Z 门操作。
若 Alice 的测量结果为 \( \left\lvert 11 \right\rangle \)，Bob 持有的量子态为 \( \alpha \left\lvert 1 \right\rangle - \beta \left\lvert 0 \right\rangle \)，Bob 需要对自己持有的量子态进行 X 门和 Z 门操作。

SWAP 门和 CSWAP 门¶

SWAP 门交换两个量子比特的状态，CSWAP 门在 SWAP 门的基础上增加了一个控制量子比特。

\[ \mathrm{SWAP} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

Example

作用于两量子比特系统 \( \left\lvert q_0 q_1 \right\rangle \) 上，其中

\[ \left\lvert q_0 \right\rangle = \begin{bmatrix} \alpha_1 \\ \beta_1 \end{bmatrix}, \left\lvert q_1 \right\rangle = \begin{bmatrix} \alpha_2 \\ \beta_2 \end{bmatrix} \]

作用 SWAP 门后，量子系统变为

\[ \mathrm{SWAP} \left\lvert q_0 q_1 \right\rangle = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \alpha_1 \alpha_2 \\ \alpha_1 \beta_2 \\ \beta_1 \alpha_2 \\ \beta_1 \beta_2 \end{bmatrix} = \begin{bmatrix} \alpha_1 \alpha_2 \\ \beta_1 \alpha_2 \\ \alpha_1 \beta_2 \\ \beta_1 \beta_2 \end{bmatrix} = \left\lvert q_1 q_0 \right\rangle \]

Toffoli 门¶

Toffoli 门是 CCNOT 门，作用于三量子比特系统，当两个控制量子比特均为 \( \left\lvert 1 \right\rangle \) 时，对目标量子比特施加 X 门。

量子系统的并行性¶

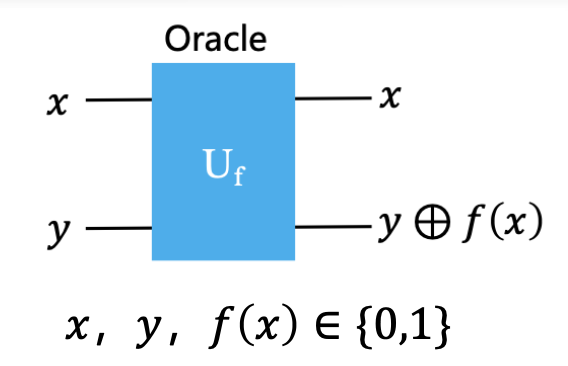
量子并行性是量子计算的一个基本特征，它使得量子计算机可以同时计算 \(f(x)\) 在多个 \(x\) 取值下的函数值。

设存在一个量子电路可以实现 \(\left\lvert x, y \right\rangle \rightarrow \left\lvert x, y \oplus f(x) \right\rangle\) 的变换，其中 \(\oplus\) 表示模 2 加法（异或运算）。

那么若 \(\left\lvert x \right\rangle = \frac{1}{\sqrt{2}} \left( \left\lvert 0 \right\rangle + \left\lvert 1 \right\rangle \right)\) 为叠加态，且 \(\left\lvert y \right\rangle = \left\lvert 0 \right\rangle\)，则经过该量子电路后，量子态变为

\[ \frac{1}{\sqrt{2}} \left( \left\lvert 0, f(0) \right\rangle + \left\lvert 1, f(1) \right\rangle \right) \]

这意味着量子计算机可以同时计算 \(f(0)\) 和 \(f(1)\) 的值。

若输入 \(x\) 为多量子比特，则对 \(x\) 中每个量子比特施加 Hadamard 门，然后对 \(x\) 和 \(y\) 进行量子并行计算。

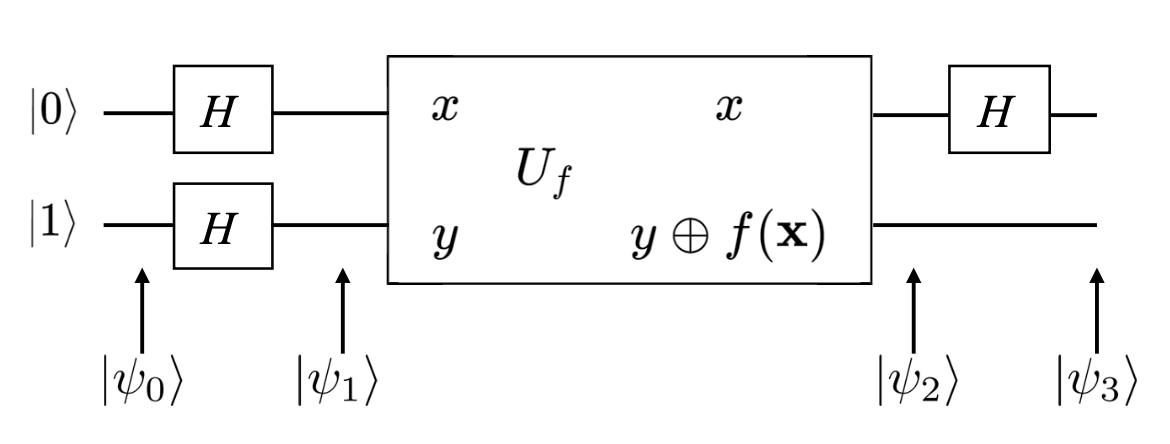
Deutsch 算法¶

Deutsch 算法是量子计算的第一个量子算法，用于判断一个函数 \(f(x)\) 是否是常函数（对于所有输入都输出相同值）或者平衡函数（对于一半输入输出 0，另一半输入输出 1）。

经典算法¶

对于 n 位输入 \(x\)，需要查询 \(2^{n-1} + 1\) 次才能判断函数 \(f(x)\) 是否是常函数或者平衡函数。

量子算法¶

先考虑单量子比特的情况，函数 \(f(x)\) 有四种可能：

平衡函数：\(f(x) = \neg x, f(x) = x\)
常数函数：\(f(x) = \left\lvert 0 \right\rangle, f(x) = \left\lvert 1 \right\rangle\)

Deutsch 算法的量子电路如下：

初始化量子比特为 \( \left\lvert 01 \right\rangle \)。

对两个量子比特施加 Hadamard 门得到

\[ \left\lvert \psi_1 \right\rangle = \frac{1}{2} \left( \left\lvert 0 \right\rangle + \left\lvert 1 \right\rangle \right) \left( \left\lvert 0 \right\rangle - \left\lvert 1 \right\rangle \right) \]

由于异或运算的特性，得

\[ \left\lvert x, y \right\rangle \rightarrow \left\lvert x, y \oplus f(x) \right\rangle = \left\lvert x \right\rangle (-1)^{f(x)} \left\lvert y \right\rangle \]

得到

\[ \begin{aligned} \left\lvert \psi_2 \right\rangle &= U_f \frac{1}{\sqrt{2}} \left( \left\lvert 0 \right\rangle + \left\lvert 1 \right\rangle \right) \left\lvert y \right\rangle \\ &= \frac{1}{\sqrt{2}} \left( U_f \left\lvert 0 \right\rangle \left\lvert y \right\rangle + U_f \left\lvert 1 \right\rangle \left\lvert y \right\rangle \right) \\ &= \frac{1}{\sqrt{2}} \left( \left\lvert 0 \right\rangle (-1)^{f(0)} \left\lvert y \right\rangle + \left\lvert 1 \right\rangle (-1)^{f(1)} \left\lvert y \right\rangle \right) \\ &= \frac{\left\lvert 0 \right\rangle (-1)^{f(0)} + \left\lvert 1 \right\rangle (-1)^{f(1)}}{\sqrt{2}} \left\lvert y \right\rangle \end{aligned} \]

分类讨论可知

\[ \left\lvert \psi_2 \right\rangle = \begin{cases} \pm \left[ \frac{\left\lvert 0 \right\rangle + \left\lvert 1 \right\rangle}{\sqrt{2}} \right] \left[ \frac{\left\lvert 0 \right\rangle - \left\lvert 1 \right\rangle}{\sqrt{2}} \right], & \text{if}\ f(0) = f(1) \\ \pm \left[ \frac{\left\lvert 0 \right\rangle - \left\lvert 1 \right\rangle}{\sqrt{2}} \right] \left[ \frac{\left\lvert 0 \right\rangle - \left\lvert 1 \right\rangle}{\sqrt{2}} \right], & \text{if}\ f(0) \neq f(1) \end{cases} \]

对第一个量子比特施加 Hadamard 门，得到

\[ \left\lvert \psi_3 \right\rangle = \begin{cases} \pm \left\lvert 0 \right\rangle \left[ \frac{\left\lvert 0 \right\rangle - \left\lvert 1 \right\rangle}{\sqrt{2}} \right], & \text{if}\ f(0) = f(1) \\ \pm \left\lvert 1 \right\rangle \left[ \frac{\left\lvert 0 \right\rangle - \left\lvert 1 \right\rangle}{\sqrt{2}} \right], & \text{if}\ f(0) \neq f(1) \end{cases} = \pm \left\lvert f(0) \oplus f(1) \right\rangle \left[ \frac{\left\lvert 0 \right\rangle - \left\lvert 1 \right\rangle}{\sqrt{2}} \right] \]

测量第一个量子比特，若测量结果为 \( \left\lvert 0 \right\rangle \)，则函数为常函数；若测量结果为 \( \left\lvert 1 \right\rangle \)，则函数为平衡函数。

Oracle¶

Oracle 是一个黑盒子，用于描述一个函数的作用，只知道行为，不知道内部实现。

量子计算中，Oracle 的功能 \(f\) 可以表示为

\[ f(\left\lvert \Psi \right\rangle) = \begin{cases} \left\lvert 1 \right\rangle, & \text{if}\ \left\lvert \Psi \right\rangle \in \text{certian set}\ S \\ \left\lvert 0 \right\rangle, & \text{else} \end{cases} \]

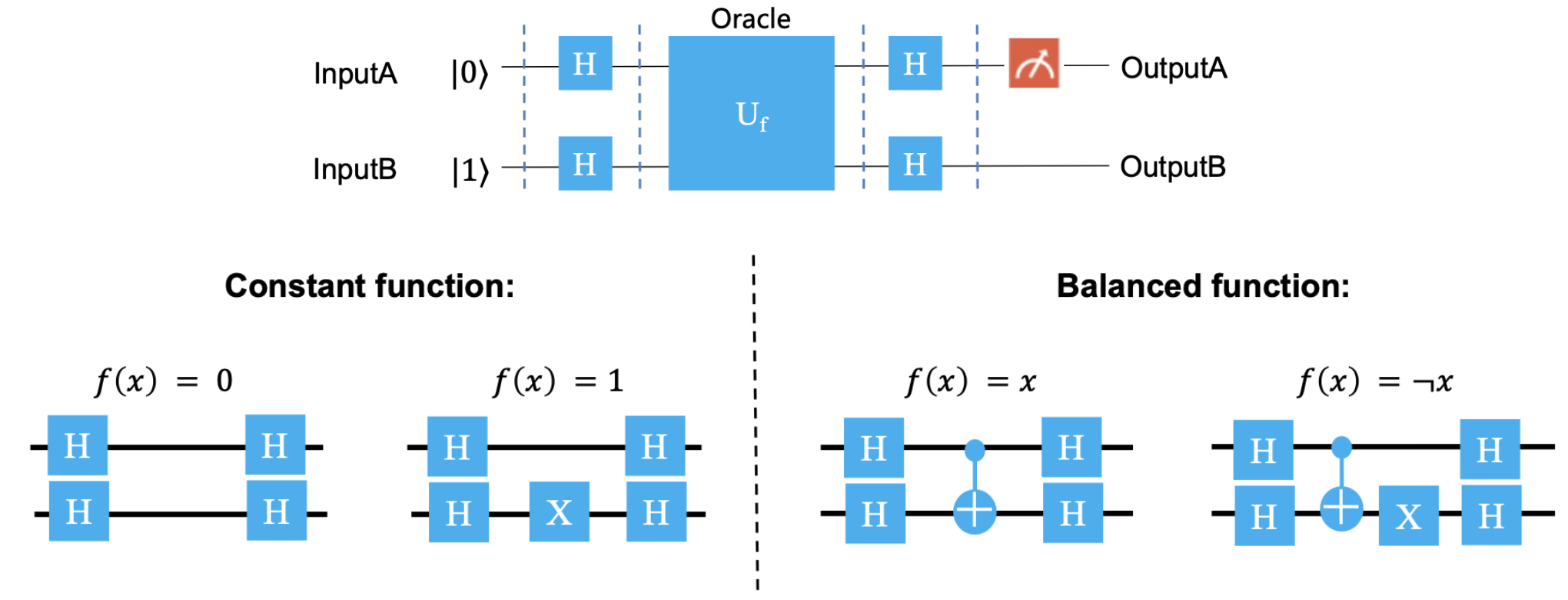
Oracle 线路设计¶

其中 Input A 为固定的 \(\left\lvert 0 \right\rangle\)，Output A 为操作结果，Output B 为冗余输出。

根据 \(f\) 的定义，可以得到上图四种 Oracle 线路。

Oracle 线路简化¶

简化规则：

\(HH = I\)
\(HXH = Z\)
CNOT 简化：

根据控制比特为高位比特还是低位比特，CNOT 门可以分为两种：

\[ \mathrm{CNOT}_{\text{low}} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} , \mathrm{CNOT}_{\text{high}} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} \]

简化规则：

\[ (H \otimes H) \mathrm{CNOT}_{\text{low}} (H \otimes H) = \mathrm{CNOT}_{\text{high}} \]

写出矩阵形式可以验证。

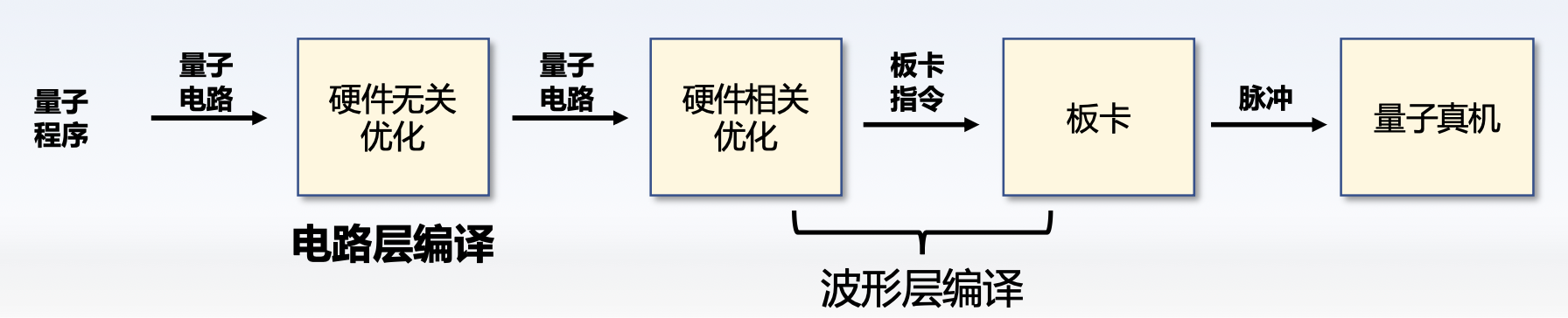
量子电路部署流程¶

波形生成：每种基础门都有其对应的波形，将量子门转换成量子芯片可识别的波形是波形层编译的一部分。两比特量子门则每个比特有两段波形，单门波形一般只有一段。