量子测量与量子图灵机¶

量子态演化¶

波函数¶

波函数是量子力学的基本假设，最简单的形式是 \(\phi(x) = Ae^{i(p/\hbar)x}\)，表示了粒子在某一位置的概率幅。\(\lVert \phi(x) \rVert^2\) 表示了粒子在该位置的概率密度。满足归一化条件，即对整个空间积分为 1。

哈密顿量¶

表示为 \(H\)，是一个厄米算符。作用于系统的波函数上，产生系统的能量和动力学演化。

由动力项和势能项组成。

动能项描述了系统中粒子的运动能量，通常用动量算符和质量来表示。
势能项描述了系统中粒子之间的相互作用和受到的外部场的影响，可以是位置算符和外部势场的函数。

\[ \hat{H} = -\frac{\hbar^2}{2m} \nabla^2 + V(\bar{r}) \]

哈密顿量表达式的第一项实则为粒子的动能，第二项是一个空间位置的函数，即势能函数，表示粒子处在不同位置时的势能。

\[ \hat{H} = \hat{T} + \hat{V} = \frac{\mathbf{\hat{p}}^2}{2m} + V(\mathbf{r}, t) = -\frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r}, t) \]

哈密顿量的本征值是系统能量的可能取值，对应的特征向量是在该能量取值下的状态向量。

薛定谔方程与量子态演化¶

\(H\) 可以和时间有关，也可以独立与时间。若与时间独立，则薛定谔方程为：

\[ i\hbar \frac{\mathrm{d}}{\mathrm{d}\ t} \left\lvert \psi(t) \right\rangle = \hat{H} \left\lvert \psi(t) \right\rangle \]

移项后积分：

\[ \begin{aligned} \int_{t_1}^{t_2} \frac{i\hbar}{\left\lvert \psi(t) \right\rangle} \mathrm{d} \left\lvert \psi(t) \right\rangle &= \int_{t_1}^{t_2} \hat{H} \mathrm{d} t \\ i\hbar (\ln \left\lvert \psi(t_2) \right\rangle - \ln \left\lvert \psi(t_1) \right\rangle) &= \hat{H} (t_2 - t_1) \end{aligned} \]

得到：

\[ \left\lvert \psi(t_2) \right\rangle = e^{\frac{-i\hat{H}\Delta t}{\hbar}} \left\lvert \psi(t_1) \right\rangle \]

设 \(t_1 = 0, t_2 = t\)，则：

\[ \left\lvert \psi(t) \right\rangle = e^{\frac{-i\hat{H}t}{\hbar}} \left\lvert \psi(0) \right\rangle = U \left\lvert \psi(0) \right\rangle \]

该式表明，量子态从初态到终态的演化可以由一个与 \(H\) 有关的算子表示，该算子又被称为时间演化算子 \(U\)，且 \(U\) 一定是幺正的。

线性与非线性量子态演化¶

根据量子力学原理，量子态演化过程由两部分组成：

线性演化过程：如果一个物理系统没有被测量，它将按照薛定谔方程以一种确定的、线性的方式演化。
非线性演化过程：如果对系统进行一个测量，系统将立即非线性地、随机地从初始的叠加态跃迁到正被测量的可观测量的一个本征态，这时，实验者就会感知到一个确定的观察值，即本征态相应的本征值。

即作用量子门时，量子态的演化是线性的，而测量量子态时，量子态的演化是非线性的。

量子测量¶

特征值与特征向量的几何意义¶

矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值。

特征值分解¶

向量 \(\mathbf{v}\) 是矩阵 \(A\) 的特征向量，对应的特征值是 \(\lambda\)，则有：

\[ A\mathbf{v} = \lambda \mathbf{v} \]

特征值分解：

\[ A = Q \Lambda Q^{-1} \]

其中 \(\Lambda\) 是一个对角矩阵，对角线上的元素是矩阵 \(A\) 的特征值，\(Q\) 是 \(A\) 的特征向量组成的矩阵。

特征值分解的含义¶

矩阵 \(A\) 的信息可以由其特征值和特征向量表示。

对于矩阵为高维的情况下，通过特征值分解得到的前 N 个特征向量，就对应了这个矩阵最主要的 N 个变化方向。利用这前 N 个变化方向，就可以近似这个矩阵（变换）。

量子计算中的特征分解（谱分解）¶

只有对可对角化矩阵才可以施以特征分解。特征值的集合 \(\{\lambda_i\}\)，也称为“谱”（Spectrum）。厄米矩阵（共轭对称的方阵）属于正规矩阵，根据正规矩阵的性质可知，其可以对角化。

假设 \(A\) 是一个复数域上的正规矩阵，特征值为 \(\{\lambda_i\}\)，标准正交基为 \(\{\left\lvert e_i\right\rangle\}\)，则有：

\[ A = \sum_i^n \lambda_i \left\lvert e_i \right\rangle \left\langle e_i \right\rangle \]

标准正交基的完备性方程为：

\[ \sum_i^n \left\lvert e_i \right\rangle \left\langle e_i \right\rvert = I \]

可通过完备性方程检验一组基是否是标准正交基。

投影算子¶

定义投影到单位向量 \(\left\lvert e_k \right\rangle\) 上的投影算子为：

\[ P_k = \left\lvert e_k \right\rangle \left\langle e_k \right\rvert \]

满足性质：

\(P_k^2 = P_k\)
\(P_k P_j = \delta_{kj} P_k\)
\(\sum_k P_k = I\)

则复数域上的正规矩阵 \(A\) 可以表示为：

\[ A = \sum_i^n \lambda_i \left\lvert e_i \right\rangle \left\langle e_i \right\rvert = \sum_i^n \lambda_i P_i \]

因此 \(A\) 作用于任何向量，其几何意义为：该向量投影到 \(A\) 的各特征向量上，然后再以特征值 \(\lambda_i\) 为权重进行线性组合。

量子测量¶

一般测量
投影测量
POVM 测量

对于选定的观测性质，我们需要执行相应的测量算符。每个可能的测量结果都对应一个测量算符的特征值 \(\lambda_i\)，由可观测量 \(\lvert P\left\lvert \psi \right\rangle \rvert^2\) 描述。

投影测量的可观测量¶

可观测量由 \(A\) 表示，为待观测系统上的厄米算子，可以写成谱分解的形式：

\[ A = \sum_i^n \lambda_i P_i \]

测量的可能结果与 \(A\) 的特征值 \(\lambda_i\) 相对应。对状态 \(\left\lvert \psi \right\rangle\) 进行测量，得到的结果 \(i\) 的概率为：

\[ p_i = p(\lambda = \lambda_i) = \left\langle \psi \right\lvert P_i^\dagger P_i \left\lvert \psi \right\rangle = \left\langle \psi \right\lvert P_i \left\lvert \psi \right\rangle \]

测量后的态坍缩为：

\[ \frac{P_i \left\lvert \psi \right\rangle}{\sqrt{p_i}} \]

观测量的平均值为：

\[ E(A) = \sum_i^n \lambda_i p_i = \left\langle \psi \right\lvert A \left\lvert \psi \right\rangle = \left\langle A \right\rangle \]

标准差：

\[ \Delta(A) = \sqrt{\left\langle (A - \left\langle A \right\rangle)^2 \right\rangle} = \sqrt{\left\langle A^2 \right\rangle - \left\langle A \right\rangle^2} \]

投影测量的测量算子¶

量子测量由投影算子的集合 \(\{P_i\}\) 描述，投影算子是一类特殊的厄米算符，它的本征值为 0 或 1，其本征态形成了正交归一的完备基。

指标(index) \(i\) 表示在实验上可能发生的结果。如果测量前的量子系统处在最新状态 \(\left\lvert \psi \right\rangle\)，那么结果发生的概率为:

\[ p_i = \left\lvert P_i \left\lvert \psi \right\rangle \right\rvert^2 = \left\langle \psi \right\lvert P_i^\dagger P_i \left\lvert \psi \right\rangle = \left\langle \psi \right\lvert P_i \left\lvert \psi \right\rangle \]

设 \(P_i\) 的本征态为 \(\left\lvert \alpha \right\rangle\)，则概率还可以表示为：

\[ p_\alpha = \left\lvert \left\langle \psi \lvert \alpha \right\rangle \right\rvert^2 \]

量子线路和测量操作¶

把测量操作作为量子线路的一部分，有时也被称为测量门，原理即投影测量。

双比特量子电路整体测量

对于如下的双比特量子电路：

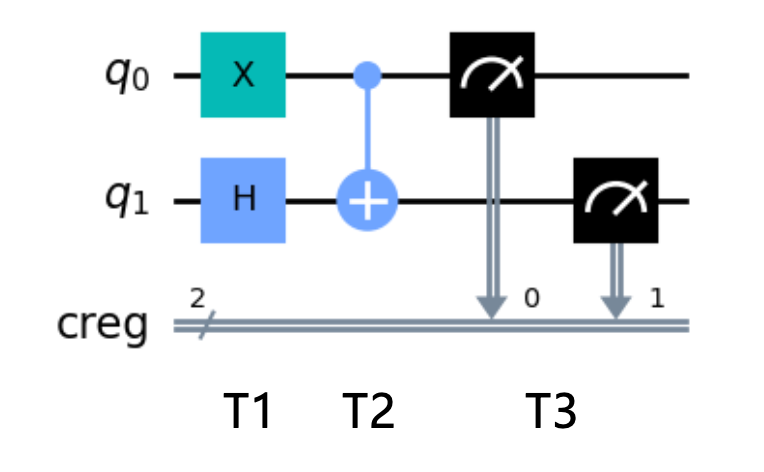
对其进行整体测量：

T1 时刻：

\[ \begin{aligned} \left\lvert \psi_1 \right\rangle &= (X \otimes H) \left\lvert 00 \right\rangle \\ &= ( \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \otimes \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} ) \left\lvert 00 \right\rangle \\ &= \frac{1}{\sqrt{2}} \begin{bmatrix} 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & -1 \\ 1 & 1 & 0 & 0 \\ 1 & -1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} \\ &= \frac{1}{\sqrt{2}} \begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \end{bmatrix} \\ &= \frac{1}{\sqrt{2}} (\left\lvert 10 \right\rangle + \left\lvert 11 \right\rangle) \end{aligned} \]
T2 时刻，经过 CNOT 门：

\[ \begin{aligned} \left\lvert \psi_2 \right\rangle &= \mathrm{CNOT} \left\lvert \psi_1 \right\rangle \\ &= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \end{bmatrix} \\ &= \frac{1}{\sqrt{2}}(\left\lvert 10 \right\rangle + \left\lvert 11 \right\rangle) \end{aligned} \]
T3 时刻，进行整体测量，分别作用四个投影算子。
- 使用测量操作 \(M_{00} = \left\lvert 00 \right\rangle \left\langle 00 \right\rvert\)，测量结果为 00 的概率为：
  
  \[ \begin{aligned} P(\left\lvert 00 \right\rangle) &= \left\langle \psi_2 \right\lvert M_{00}^\dagger M_{00} \left\lvert \psi_2 \right\rangle \\ &= \left\langle \psi_2 \right\lvert M_{00} \left\lvert \psi_2 \right\rangle \\ &= \frac{1}{\sqrt{2}} \begin{bmatrix} 0 & 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \end{bmatrix} \\ &= 0 \end{aligned} \]
  
  可知，量子态不可能坍缩到 \(\left\lvert 00 \right\rangle\)。
- 其他三种情况同理。

双比特量子电路部分测量

对于如下的双比特量子电路：

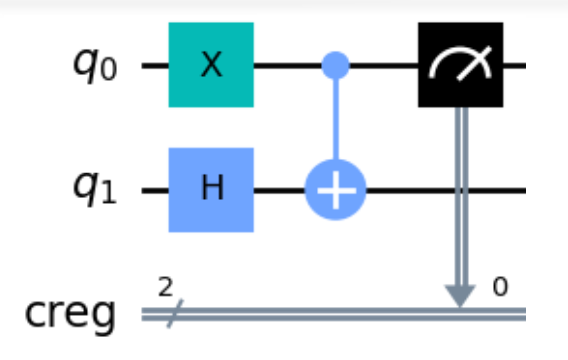
只对低位量子比特进行测量，则此时的两种测量矩阵为：

\[ \begin{aligned} M_{0}^{q_0} &= M_{00} + M_{01} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} + \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \\ M_{1}^{q_0} &= M_{10} + M_{11} = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} + \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{aligned} \]

测量后得到的概率分别为：

\[ \begin{aligned} P_{q_0}(\left\lvert 0 \right\rangle) &= \left\langle \psi_2 \right\lvert M_{0}^{q_0} \left\lvert \psi_2 \right\rangle = \frac{1}{\sqrt{2}} \begin{bmatrix} 0 & 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \end{bmatrix} = 0 \\ P_{q_0}(\left\lvert 1 \right\rangle) &= \left\langle \psi_2 \right\lvert M_{1}^{q_0} \left\lvert \psi_2 \right\rangle = \frac{1}{\sqrt{2}} \begin{bmatrix} 0 & 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix} 0 \\ 0 \\ 1 \\ 1 \end{bmatrix} = 1 \end{aligned} \]

测量后，量子态坍缩为

\[ \left\lvert \psi_3 \right\rangle = \frac{M_{1}^{q_0} \left\lvert \psi_2 \right\rangle}{\sqrt{P_{q_0}(\left\lvert 1 \right\rangle)}} = \frac{1}{\sqrt{2}}(\left\lvert 10 \right\rangle + \left\lvert 11 \right\rangle) \]

量子态区分公设¶

量子测量的原理的一大应用是区分量子系统中不同的量子态。

如果一组态向量 \(\{\left\lvert \psi_i \right\rangle\}\) 是正交的，那么可以定义测量算子 \(M_i = \left\lvert \psi_i \right\rangle \left\langle \psi_i \right\rvert\)，对于其中的一个未知角标的态向量 \(\left\lvert \psi_k \right\rangle\)，用这组测量算子进行测量，只有当 \(i = k\) 时，有：

\[ p(i) = \left\langle \psi_i \right\lvert M_i \left\lvert \psi_i \right\rangle = 1 \]

其他情况下，有 \(p(i) = 0\)。这样就可以区分出不同的量子态。
如果态向量不正交，则不存在一组测量算子可以完全区分这些态向量，因为一个态向量可以分解为其他态向量上的分量，导致 \(p(i) < 1\)。

通用量子门¶

通用量子门（Universal Quantum Gate）是一种能够在量子计算中实现任意量子操作的门。

以下的门集合是通用的：

单量子比特门和 CNOT 门是通用的。
通用门的标准集合，由 H 门、相位门、CNOT 门和 \(\pi/8\) 门组成。
H 门、相位门、CNOT 门和 Toffoli 门。

量子门分解¶

通用量子门可以用来对任意的酉操作进行近似。这种近似的方法被称为量子门分解（Quantum Gate Decomposition）或量子门逼近（Quantum Gate Approximation）。

基本思想：将目标酉操作分解为一系列更简单的量子门的乘积，通过合理选择和组合这些基本量子门，并对它们的参数进行调整，我们可以逐步逼近目标酉操作。

分解的精度取决于所使用的门集合和逼近方法的复杂程度。通常情况下，使用更多的门和更复杂的门序列可以提供更精确的逼近结果。

常见的量子门分解方法包括：

应用基于泰勒级数展开的逼近方法，将目标酉操作近似为一系列基本门的乘积。
利用通用量子门集合中的门进行分解。
使用优化算法，例如基于梯度下降的方法，找到适合的门序列和参数来逼近目标酉操作。

量子门分解代价¶

Solovay-Kitaev 定理表明，对任意的单量子比特门，如果要求精度为 \(\epsilon\)，则需要 \(\mathcal{O}(\log^c(1/\epsilon))\) 个门来逼近。对于有 \(m\) 个门的量子系统以及精度为 \(\epsilon\) 的近似，需要 \(\mathcal{O}(m \log^c(m/\epsilon))\) 个门。

量子图灵机和量子电路模型¶

没啥写的。