量子算法
量子傅立叶变换
离散傅立叶变换
将离散信号从时域转换到频域。
离散傅立叶变换:
\[
\begin{aligned}
&\{x_j\} \xrightarrow{\mathrm{DFT}} \{y_k\} \\
&y_k = \frac{1}{\sqrt{N}} \sum_{j=0}^{N-1} x_j e^{\frac{2\pi i}{N} jk}
\end{aligned}
\]
逆离散傅立叶变换:
\[
\begin{aligned}
&\{y_k\} \xrightarrow{\mathrm{IDFT}} \{x_j\} \\
&x_j = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} y_k e^{-\frac{2\pi i}{N} jk}
\end{aligned}
\]
量子傅立叶变换
量子傅里叶变换(QFT)的作用是将量子态从计算基 \(\{\left\lvert j \right\rangle\}\) 转换到频域基 \(\{\left\lvert k \right\rangle\}\) 。振幅序列 \(\{x_j\}\) 被转换为 \(\{y_k\}\)
\[
\begin{aligned}
&\sum_{j=0}^{N-1} x_j \left\lvert j \right\rangle \xrightarrow{\mathrm{QFT}} \sum_{k=0}^{N-1} y_k \left\lvert k \right\rangle \\
&y_k = \frac{1}{\sqrt{N}} \sum_{j=0}^{N-1} x_j e^{\frac{2\pi i}{N} jk}
\end{aligned}
\]
作为量子算符为:
\[
\mathrm{QFT}\left\lvert j \right\rangle = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{\frac{2\pi i}{N} jk} \left\lvert k \right\rangle
\]
QFT 的张量基形式
规定记法:
基态 \(\left\lvert j \right\rangle\) 表示为 \(\left\lvert \overline{j_1 j_2 \cdots j_n} \right\rangle\) ,其中 \(j = j_1 2^{n-1} + j_2 2^{n-2} + \cdots + j_n 2^0\) 。
\(\overline{0.j_1 j_2 \cdots j_n}\) 表示二进制小数 \(j_1 2^{-1} + j_2 2^{-2} + \cdots + j_n 2^{-n}\) 。
使用 \(n\) 个量子比特进行 QFT,共有 \(N = 2^n\) 个基态。QFT 可以写成:
\[
\begin{aligned}
\mathrm{QFT}\left\lvert j \right\rangle &= \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{\frac{2\pi i}{N} jk} \left\lvert k \right\rangle \\
\mathrm{QFT}\left\lvert \overline{j_1 j_2 \cdots j_n} \right\rangle &= \frac{1}{\sqrt{2^n}} (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.j_n}} \left\lvert 1 \right\rangle) \otimes \cdots \otimes (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.j_1 j_2 \cdots j_n}} \left\lvert 1 \right\rangle)
\end{aligned}
\]
Proof
\[
\begin{aligned}
\mathrm{QFT}\left\lvert j \right\rangle &= \frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} \exp(\frac{2\pi i}{2^n} jk) \left\lvert k \right\rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{k_1=0}^{1} \cdots \sum_{k_n=0}^{1} \exp(\frac{2\pi i}{2^n} j \sum_{l=1}^{n} k_l 2^{n-l}) \left\lvert k_1 k_2 \cdots k_n \right\rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{k_1=0}^{1} \cdots \sum_{k_n=0}^{1} \bigotimes_{l=1}^{n} \exp(\frac{2\pi i}{2^n} j k_l 2^{n-l}) \left\lvert k_l \right\rangle \\
&= \frac{1}{\sqrt{2^n}} \bigotimes_{l=1}^{n} \sum_{k_l=0}^{1} \exp(\frac{2\pi i}{2^n} j k_l 2^{n-l}) \left\lvert k_l \right\rangle \\
&= \frac{1}{\sqrt{2^n}} \bigotimes_{l=1}^{n} (\left\lvert 0 \right\rangle + \exp(2\pi i j 2^{-l}) \left\lvert 1 \right\rangle)
\end{aligned}
\]
由于 \(e^{2\pi i} = 1\) ,所以可以把 \(j 2^{-l}\) 的整数部分略去,得到:
\[
\begin{aligned}
\mathrm{QFT}\left\lvert j \right\rangle &= \frac{1}{\sqrt{2^n}} (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.j_n}} \left\lvert 1 \right\rangle) \otimes \cdots \otimes (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.j_1 j_2 \cdots j_n}} \left\lvert 1 \right\rangle)
\end{aligned}
\]
单量子比特 QFT
考虑单量子比特下的 QFT:
\[
\mathrm{QFT}_1 \left\lvert j \right\rangle = \frac{1}{\sqrt{2}} \sum_{k=0}^{1} e^{\frac{2 \pi i}{2} jk} \left\lvert k \right\rangle
\]
对于 \(\left\lvert 0 \right\rangle\) 和 \(\left\lvert 1 \right\rangle\) ,有:
\[
\begin{aligned}
\mathrm{QFT}_1 \left\lvert 0 \right\rangle &= \frac{1}{\sqrt{2}} (\left\lvert 0 \right\rangle + \left\lvert 1 \right\rangle) \\
\mathrm{QFT}_1 \left\lvert 1 \right\rangle &= \frac{1}{\sqrt{2}} (\left\lvert 0 \right\rangle - \left\lvert 1 \right\rangle)
\end{aligned}
\]
所以,单量子比特的 QFT 和 Hadamard 门等价。
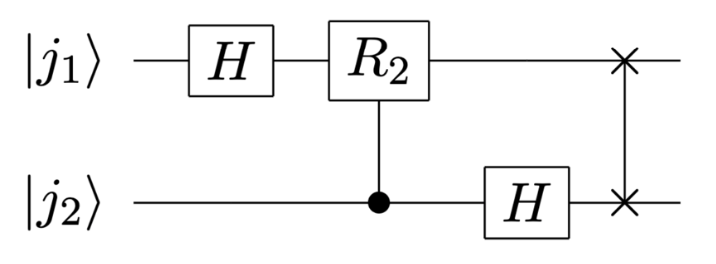
双量子比特 QFT
双量子比特下的 QFT:
\[
\mathrm{QFT}_2 \left\lvert j \right\rangle = \frac{1}{2} (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.j_2}} \left\lvert 1 \right\rangle) \otimes (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.j_1 j_2}} \left\lvert 1 \right\rangle)
\]
对于计算基 \(\left\lvert 10 \right\rangle\) 有:
\[
\begin{aligned}
\mathrm{QFT}_2 \left\lvert 10 \right\rangle &= \frac{1}{2} (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.0}} \left\lvert 1 \right\rangle) \otimes (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.10}} \left\lvert 1 \right\rangle) \\
&= \frac{1}{2} (\left\lvert 0 \right\rangle + \left\lvert 1 \right\rangle) \otimes (\left\lvert 0 \right\rangle - \left\lvert 1 \right\rangle) \\
&= \frac{1}{2} (\left\lvert 00 \right\rangle - \left\lvert 01 \right\rangle + \left\lvert 10 \right\rangle - \left\lvert 11 \right\rangle)
\end{aligned}
\]
QFT 的量子电路
定义单量子比特旋转门:
\[
R_k =
\begin{bmatrix}
1 & 0 \\
0 & e^{\frac{2\pi i}{2^k}}
\end{bmatrix}
\]
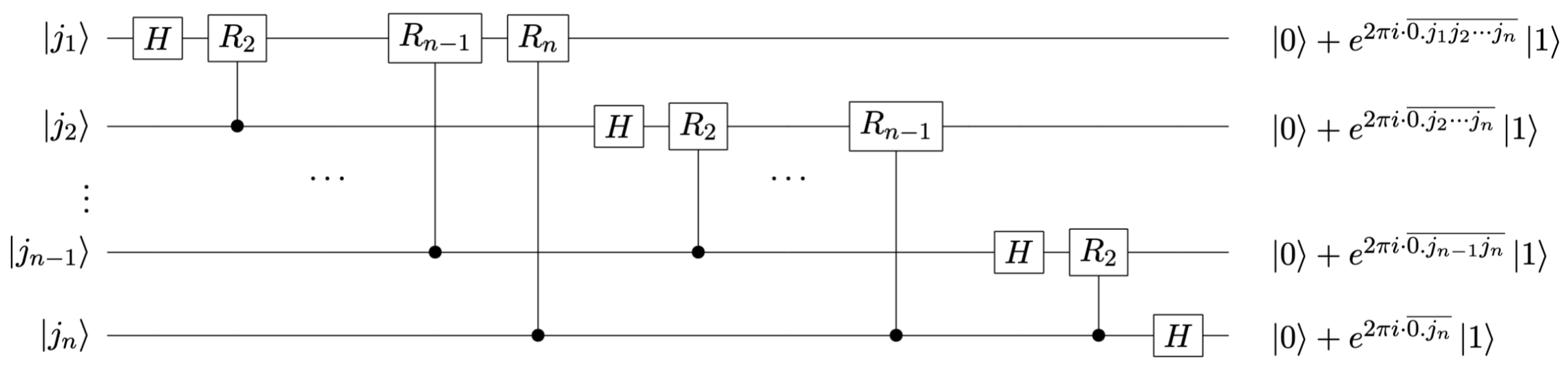
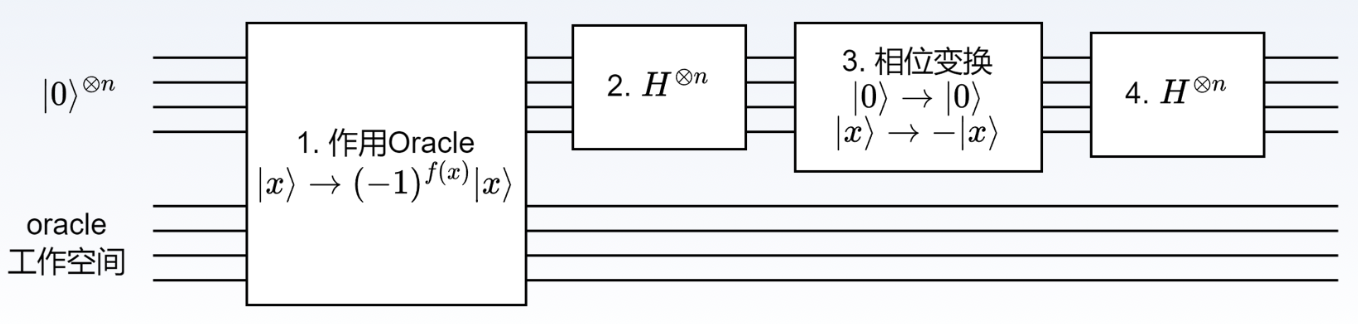
构建如下量子电路:
执行过程:
经过一个 \(H\) 门后,量子态变为 \(\frac{1}{\sqrt{2}} (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.j_1}} \left\lvert 1 \right\rangle)\left\lvert j_2 \cdots j_n \right\rangle\) 。
当 \(j_2 = \left\lvert 1 \right\rangle\) 时,执行受控旋转门 \(R_2\) ,量子态变为 \(\frac{1}{\sqrt{2}} (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.j_1 j_2}} \left\lvert 1 \right\rangle)\left\lvert j_3 \cdots j_n \right\rangle\) 。
同理,执行所有作用于第一个量子比特的受控旋转门,得到 \(\frac{1}{\sqrt{2}} (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.j_1 j_2 \cdots j_n}} \left\lvert 1 \right\rangle)\) 。
同理,最后得到 \(\frac{1}{\sqrt{2^n}} (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.j_1 j_2 \cdots j_n}} \left\lvert 1 \right\rangle)(\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.j_2 \cdots j_n}} \left\lvert 1 \right\rangle) \cdots (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.j_n}} \left\lvert 1 \right\rangle)\) 。
最后再加一系列 \(\mathrm{SWAP}\) 门,得到 QFT 的量子电路。
QFT 的量子门复杂度为 \(\mathcal{O}(n^2)\) 。
量子相位估计
量子相位估计(QPE)用于估计给定量子态的相位信息。
基本目标
已知酉矩阵 \(U\) 和其本征态 \(\left\lvert \mu \right\rangle\) ,对应本征值为 \(e^{2\pi i \varphi}\) ,估计其中相位的值 \(\varphi \in \left[0, 1\right)\) 。
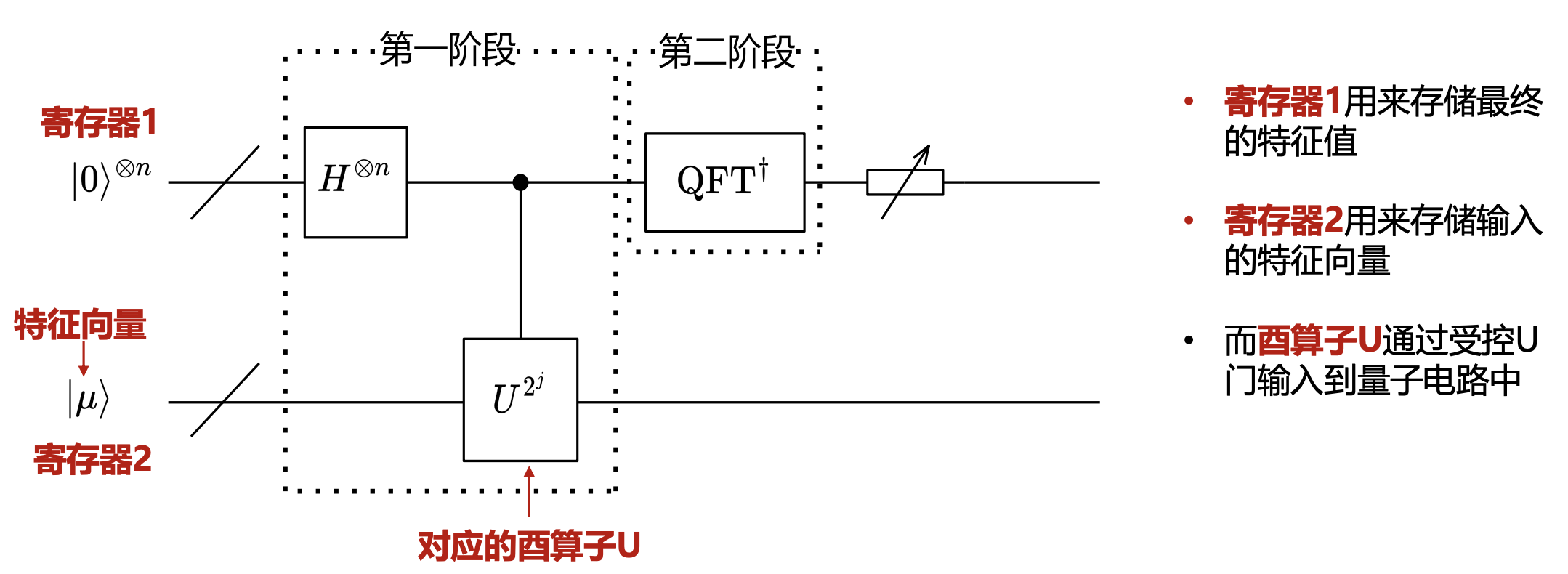
QPE 量子电路
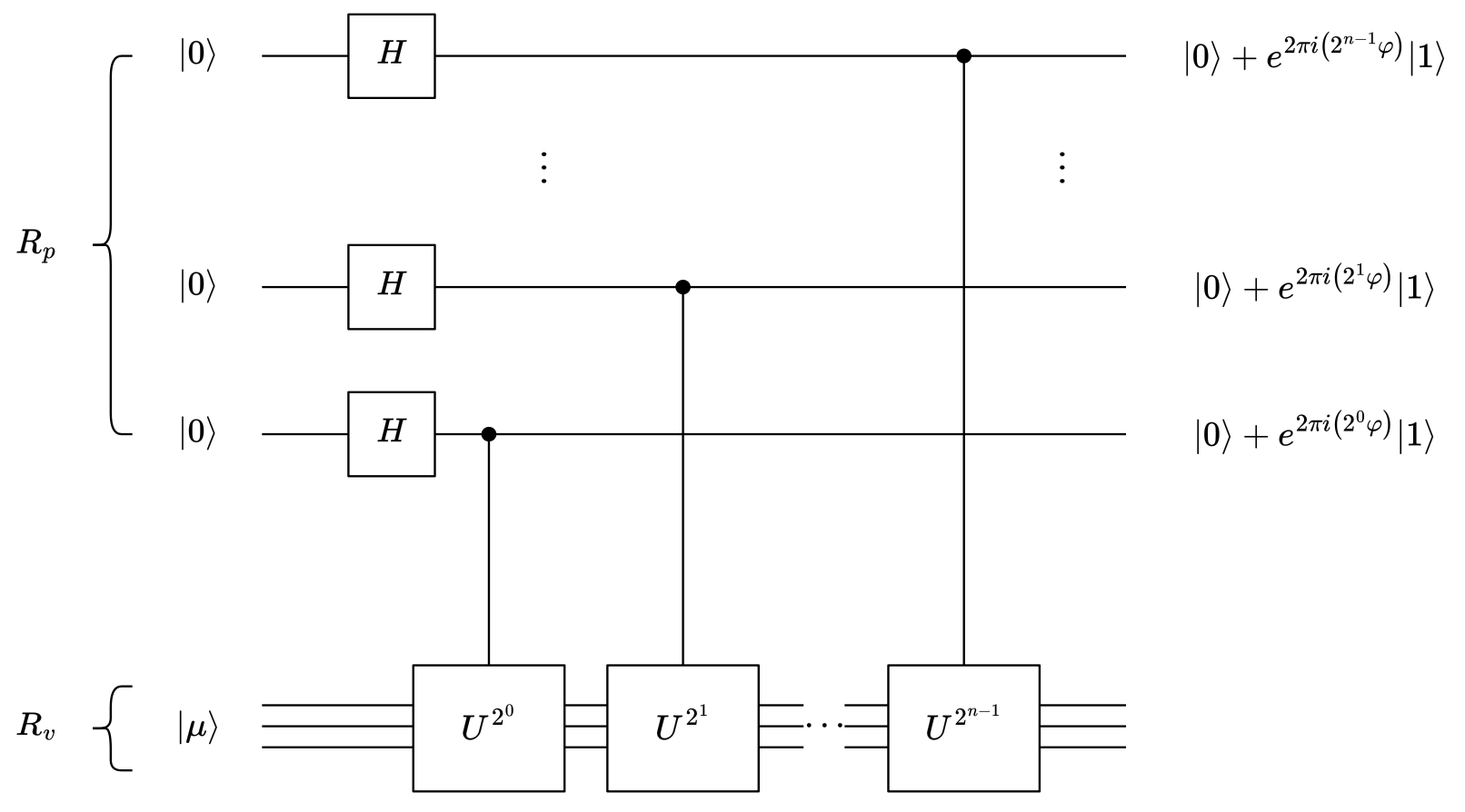
第一阶段
在 \(R_p\) 中,从下往上设量子态为 \(\left\lvert j_1 \right\rangle, \left\lvert j_2 \right\rangle, \cdots, \left\lvert j_n \right\rangle\) ,则:
\[
\left\lvert j_k \mu \right\rangle \xrightarrow{\mathrm{C-U}^{2^{k - 1}}} \left\lvert j_k \right\rangle U^{j_k 2^{k-1}} \left\lvert \mu \right\rangle
\]
因为 \(U\left\lvert \mu \right\rangle = e^{2\pi i \varphi} \left\lvert \mu \right\rangle\) ,所以:
\[
\left\lvert j_k \right\rangle U^{j_k 2^{k-1}} \left\lvert \mu \right\rangle = \frac{1}{\sqrt{2}} (\left\lvert 0 \right\rangle + e^{2\pi i 2^{k - 1} \varphi} \left\lvert 1 \right\rangle) \left\lvert \mu \right\rangle
\]
第二阶段
由 \(\varphi = \overline{0.\varphi_1 \varphi_2 \cdots \varphi_n}\) 得第一阶段结束后 \(R_p\) 的量子态为:
\[
\frac{1}{\sqrt{2^n}} (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.\varphi_n}} \left\lvert 1 \right\rangle) \otimes \cdots \otimes (\left\lvert 0 \right\rangle + e^{2\pi i \overline{0.\varphi_1 \varphi_2 \cdots \varphi_n}} \left\lvert 1 \right\rangle)
\]
最后,对 \(R_p\) 的量子态进行逆量子傅立叶变换(IQFT),得 \(\left\lvert \varphi_1 \varphi_2 \cdots \varphi_n \right\rangle\) ,从而得到 \(\varphi\) 的估计值。
Shor 算法
RSA
制造公钥和私钥:
获得两个大质数 \(p_1\) 和 \(p_2\) 。
计算 \(n = p_1 p_2\) ,\(\phi(n) = (p_1 - 1)(p_2 - 1)\) 。
取一个与 \(\phi(n)\) 互质的整数 \(e\) 。
计算 \(e\) 在模 \(\phi(n)\) 下的逆元 \(d\) ,满足 \(ed \equiv 1 \mod \phi(n)\) 。
公钥为 \((n, e)\) ,私钥为 \((n, d)\) 。
接收方计算出公钥和私钥后,将公钥发送给发送方,发送方使用公钥加密信息,接收方使用私钥解密信息。
发送方加密信息 \(a\) :\(C = a^e \mod n\) 。发送密文 \(C\) 。
接收方解密信息 \(C\) :\(a = C^d \mod n\) 。
破解 RSA 的难度在于分解 \(n\) 。
Shor 算法
Shor 算法包含经典计算和量子计算。
经典计算部分:
阶
定义 \(r = \mathrm{ord}_n(a)\) 为满足 \(a^r \equiv 1 \mod n\) 的最小正整数 \(r\) ,称为 \(a\) 关于模 \(n\) 的阶。
随机选取小于 \(n\) 的整数 \(a\) ,且 \(\gcd(a, n) = 1\) 。
计算 \(r = \mathrm{ord}_n(a)\) 。(量子计算部分)
若 \(r\) 为奇数,回到第一步。
若 \(r\) 为偶数,计算 \(x \equiv a^{r/2} \mod n\) ,则
\[
\begin{aligned}
x^2 &\equiv 1 \mod n \\
(x - 1)(x + 1) &\equiv 0 \mod n
\end{aligned}
\]
则设 \((x - 1)(x + 1) = tn = (t_1p_1)(t_2p_2)\) ,有
\[
\begin{aligned}
x - 1 &\equiv 0 \mod p_1 \Rightarrow p_1 = \gcd(x - 1, n) \\
x + 1 &\equiv 0 \mod p_2 \Rightarrow p_2 = \gcd(x + 1, n)
\end{aligned}
\]
若 \(p_1 = 1\) 或 \(p_2 = 1\) ,回到第一步。否则,得到 \(p_1\) 和 \(p_2\) 为 \(n\) 的质因数。
Shor 算法求阶
定义酉变换 \(U\) :
\[
\begin{aligned}
&U\left\lvert y \right\rangle = \left\lvert ay \mod n \right\rangle \\
\Rightarrow\ &U^2\left\lvert y \right\rangle = U\left\lvert ay \mod n \right\rangle = \left\lvert a^2 y \mod n \right\rangle \\
\Rightarrow\ &U^t\left\lvert y \right\rangle = \left\lvert a^t y \mod n \right\rangle
\end{aligned}
\]
定义量子态 \(\left\lvert u_s \right\rangle\) :
\[
\left\lvert u_s \right\rangle = \frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} e^{-\frac{2\pi i sk}{r}} \left\lvert a^k \mod n \right\rangle
\]
性质:
\(U\left\lvert u_s \right\rangle = e^{2\pi i s / r} \left\lvert u_s \right\rangle\) 。\(\displaystyle\frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} \left\lvert u_s \right\rangle = \left\lvert 1 \right\rangle\) 。
对 \(U\) 和 \(\left\lvert 1 \right\rangle\) 进行 QPE,即可等概率得到相位 \(\{0, 1/r, 2/r, \cdots, (r-1)/r\}\) 。
构造算子 \(U\) :令 \(f(x) = a^x \mod n\) ,枚举所有可能的 \(x\) ,写出变换前的量子态 \(\left\lvert x \right\rangle \left\lvert 0 \right\rangle\) ,变换后的量子态 \(\left\lvert x \right\rangle \left\lvert f(x) \right\rangle\) ,构造 \(U\) :
\[
U = \sum_{x=0}^{n-1} \left\lvert x \right\rangle \left\lvert 0 \right\rangle \left\langle x \right\rvert \left\langle f(x) \right\rvert
\]
Grover 算法
搜索算法,用于在无序数据库中搜索目标元素,将 \(\mathcal{O}(N)\) 的经典时间复杂度降低到 \(\mathcal{O}(\sqrt{N})\) 。
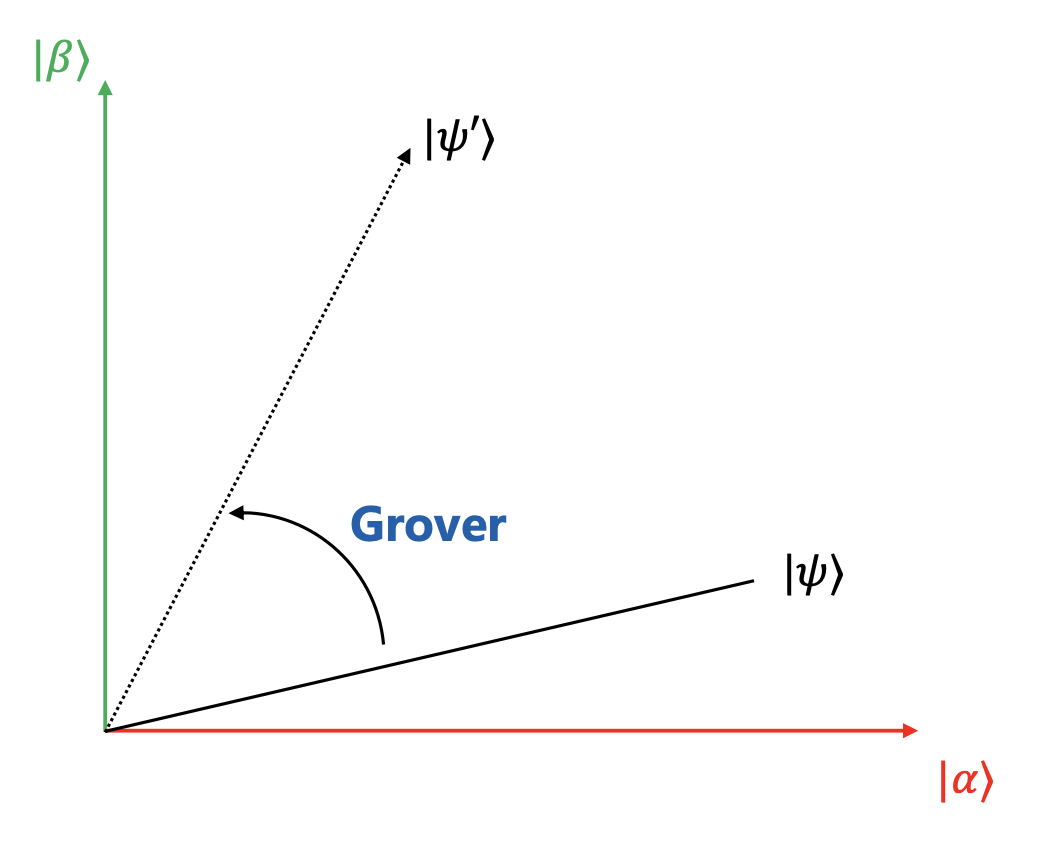
设所有正解的叠加态为 \(\left\lvert \beta \right\rangle\) ,所有错误解的叠加态为 \(\left\lvert \alpha \right\rangle\) ,则:
Grover 算法通过旋转初始量子态,使其不断接近 \(\left\lvert \beta \right\rangle\) 。
Oracle
Oracle 用于判断当前量子态是否为目标态。
\[
\left\lvert x \right\rangle \xrightarrow{\mathrm{Oracle}} (-1)^{f(x)} \left\lvert x \right\rangle
\]
其中 \(f(x) = 1\) 表示目标态,\(f(x) = 0\) 表示非目标态。
Grover 算子
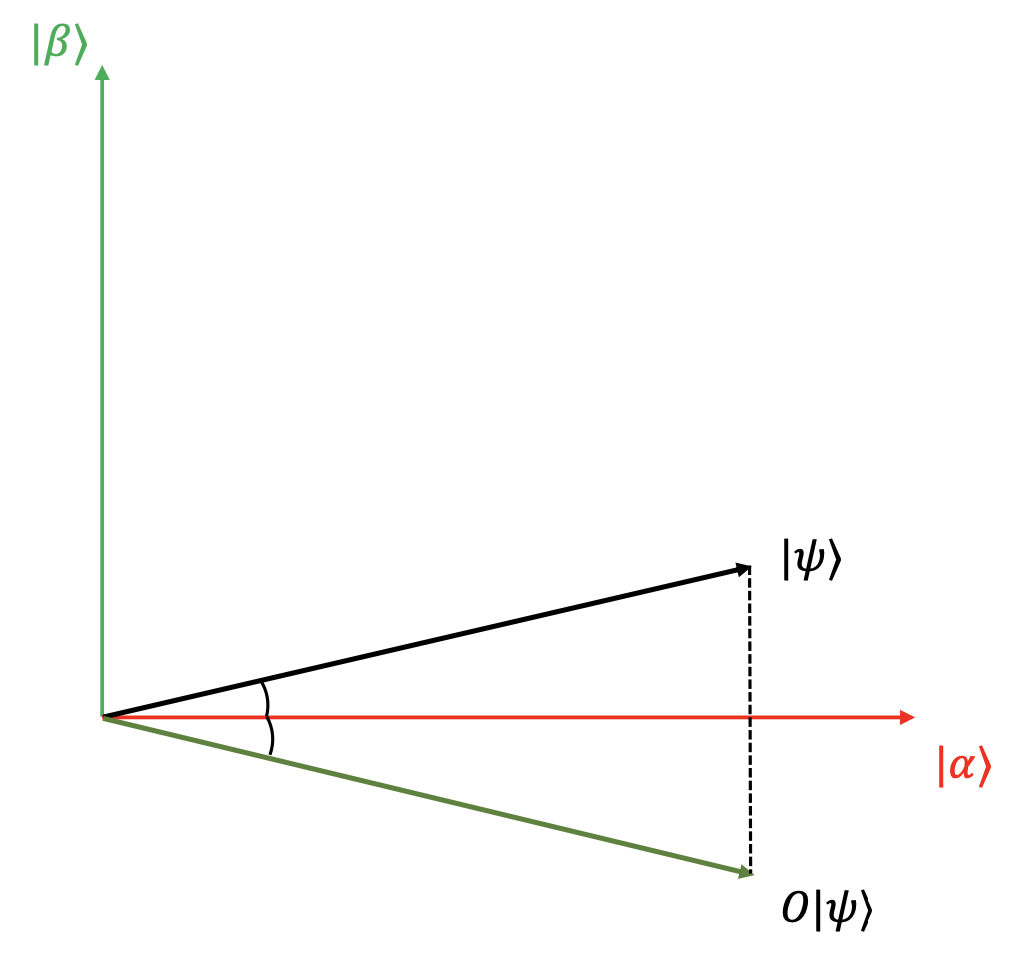
作用 Oracle
几何意义是将量子态关于 \(\left\lvert \alpha \right\rangle\) 翻转。
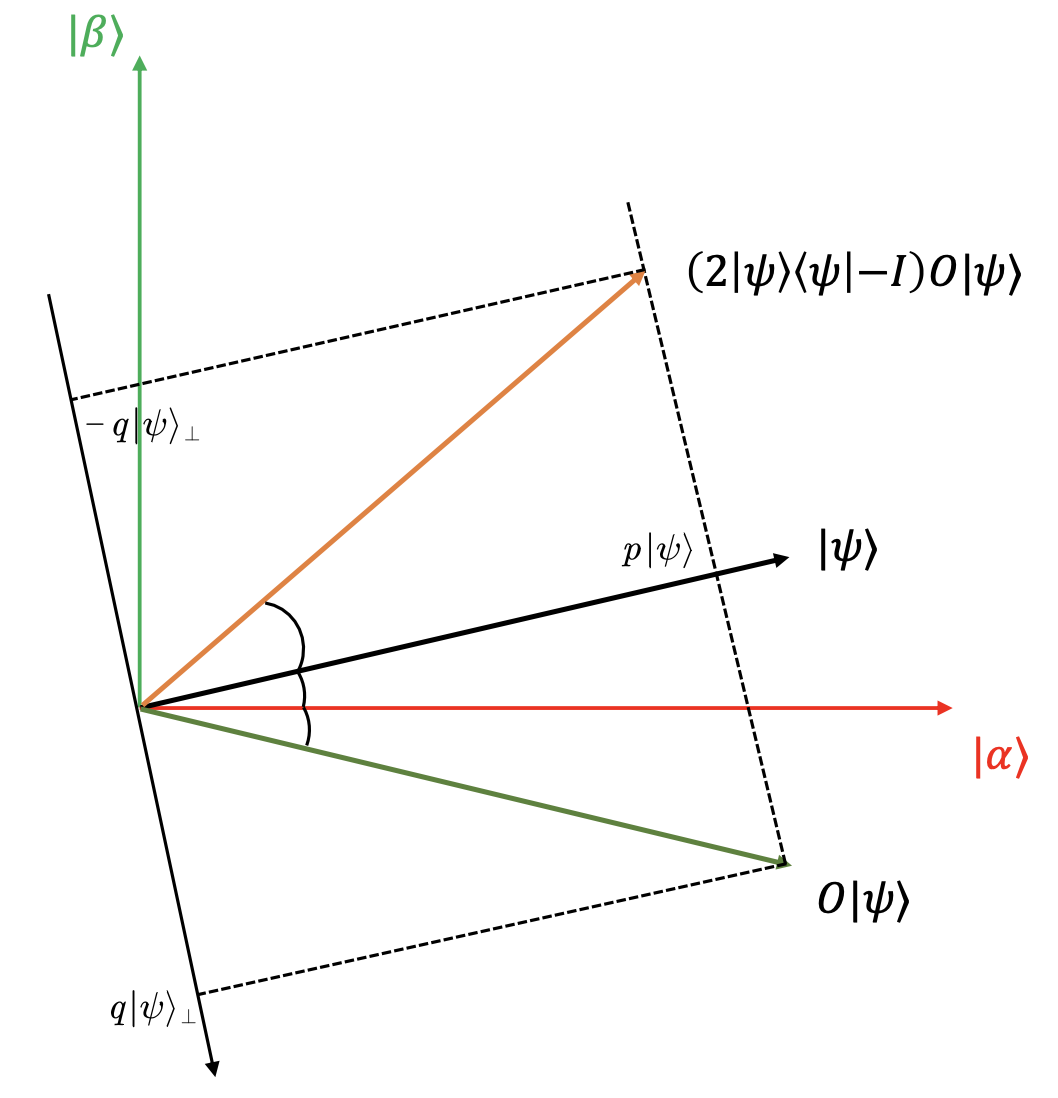
作用 Diffusion
酉矩阵表示为 \(H^{\otimes n} (2\left\lvert 0^n \right\rangle \left\langle 0^n \right\rvert - I) H^{\otimes n}\) ,令 \(\left\lvert \psi \right\rangle = H^{\otimes n} \left\lvert 0^n \right\rangle\) ,则 Diffusion 算子为 \(U_s = (2\left\lvert \psi \right\rangle \left\langle \psi \right\rvert - I)\) 。即将量子态关于 \(\left\lvert \psi \right\rangle\) 翻转。
翻转算子
设 \(\left\lvert v \right\rangle = p\left\lvert \psi \right\rangle + q\left\lvert \psi \right\rangle_{\perp}\) ,则:
\[
\begin{aligned}
U_s \left\lvert v \right\rangle &= (2\left\lvert \psi \right\rangle \left\langle \psi \right\rvert - I) (p\left\lvert \psi \right\rangle + q\left\lvert \psi \right\rangle_{\perp}) \\
&= 2p\left\lvert \psi \right\rangle \left\langle \psi \vert \psi \right\rangle + 2q\left\lvert \psi \right\rangle \left\langle \psi \right\rvert \left\lvert \psi \right\rangle_{\perp} - p\left\lvert \psi \right\rangle - q\left\lvert \psi \right\rangle_{\perp}
\end{aligned}
\]
由于归一化条件,有 \(\left\lvert \psi \vert \psi \right\rangle = 1\) ,所以
\[
\begin{aligned}
U_s \left\lvert v \right\rangle &= 2p\left\lvert \psi \right\rangle - p\left\lvert \psi \right\rangle - q\left\lvert \psi \right\rangle_{\perp} \\
&= p\left\lvert \psi \right\rangle - q\left\lvert \psi \right\rangle_{\perp}
\end{aligned}
\]
故翻转算子 \(U_s\) 的作用是将量子态关于 \(\left\lvert \psi \right\rangle\) 翻转。
几何意义
证明作用一次 G 算子,可以将量子态向目标态 \(\left\lvert \beta \right\rangle\) 旋转 \(\theta\) 角度。即
\[
G^k \left\lvert \psi \right\rangle = \cos(\frac{2k + 1}{2} \theta) \left\lvert \alpha \right\rangle + \sin(\frac{2k + 1}{2} \theta) \left\lvert \beta \right\rangle
\]
设初始态中有 \(M\) 个目标态,\(N - M\) 个非目标态,则
\[
\psi = \sqrt{\frac{N - M}{N}} \left\lvert \alpha \right\rangle + \sqrt{\frac{M}{N}} \left\lvert \beta \right\rangle
\]
则 \(\theta/2\) 为初始态与 \(\left\lvert \alpha \right\rangle\) 的夹角,有
\[
\theta = 2 \arccos(\sqrt{\frac{N - M}{N}})
\]
复杂度分析
假设 \(M \ll N\) ,则有近似
\[
\theta \approx \sin(\theta) = \frac{2\sqrt{M(N - M)}}{N} \approx 2\sqrt{\frac{M}{N}}
\]
要让量子态接近 \(\left\lvert \beta \right\rangle\) ,即令 \(\displaystyle\frac{2k + 1}{2} \theta = \frac{\pi}{2}\) ,代入上式得
\[
k = \frac{\pi}{2\theta} - \frac{1}{2} \approx \frac{\pi}{4} \sqrt{\frac{N}{M}} - \frac{1}{2} = \mathcal{O}(\sqrt{N/M})
\]
所以 Grover 算法的复杂度为 \(\mathcal{O}(\sqrt{N/M})\) 。
2024年11月11日
2024年10月28日
GoPoux4
GitHub