lab3 GEMM 通用矩阵乘法

实验步骤

Blocking & Array Packing

基准代码中，按列访问矩阵元素时局部性不高。通过对矩阵进行分块，让每个块中元素在内存中连续排列，可以提高局部性。

使用核函数 BlockCudaKernel 对矩阵 A 和矩阵 B 进行分块并存储在 _a 和 _b 中。

#define _a(_i, _j, _x, _y)                               \
  _a[((_i) * grid_size + (_j)) * block_size * block_size + ((_x) * block_size + (_y))]
#define _b(_i, _j, _x, _y)                               \
  _b[((_i) * grid_size + (_j)) * block_size * block_size + ((_x) * block_size + (_y))]

__global__ void BlockCudaKernel(double *__restrict__ _a,
                                  const double *__restrict__ a,
                                  double *__restrict__ _b,
                                  const double *__restrict__ b)
{
  int grid_size = (size + block_size - 1) / block_size;
  const int i = blockIdx.x * block_size + threadIdx.x;
  const int j = blockIdx.y * block_size + threadIdx.y;
  double a_res = 0, b_res = 0;
  if (i < size && j < size) {
    a_res = a(i, j);
    b_res = b(i, j);
  }
  _a(blockIdx.x, blockIdx.y, threadIdx.x, threadIdx.y) = a_res;
  _b(blockIdx.x, blockIdx.y, threadIdx.x, threadIdx.y) = b_res;
}

Note

此处将矩阵大小补全为 block_size 的整数倍，方便后续计算。

相应地对 MultipleCudaKernel 核函数进行修改，从分块后的矩阵拿取元素进行计算。

__global__ void MultipleCudaKernel(const double *__restrict__ _a, 
                                     const double *__restrict__ _b, 
                                     double *__restrict__ result) 
{
  int grid_size = (size + block_size - 1) / block_size;
  const int i = blockIdx.x * block_size + threadIdx.x;
  const int j = blockIdx.y * block_size + threadIdx.y;
  if (i < size && j < size) {
    double res = 0;
    for (int idx = 0; idx < gridDim.x; ++idx) {
      for (int k = 0; k < block_size && 
                      k < size - idx * block_size; ++k) {
        res += _a(blockIdx.x, idx, threadIdx.x, k) * 
               _b(idx, blockIdx.y, k, threadIdx.y);
      }
    }
    result(i, j) = res;
  }
}

核函数调用部分修改：

AdderCudaKernel<<<grid, block>>>(copy_kernel, b_kernel);
CUDA_CALL(cudaDeviceSynchronize());
double *a_block, *copy_block;
CUDA_CALL(cudaMalloc(&a_block, grid_size * grid_size * 
                               block_size * block_size * sizeof(double)));
CUDA_CALL(cudaMalloc(&copy_block, grid_size * grid_size * 
                               block_size * block_size * sizeof(double)));
BlockCudaKernel<<<grid, block>>>(a_block, a_kernel, copy_block, copy_kernel);
CUDA_CALL(cudaDeviceSynchronize());
// Perform A * B -> Result.
MultipleCudaKernel<<<grid, block>>>(a_block, copy_block, result_kernel);
CUDA_CALL(cudaDeviceSynchronize());
// Swap pointers between A and Result.
double *tmp = a_kernel;
a_kernel = result_kernel;
result_kernel = tmp;

cudaFree(a_block);
cudaFree(copy_block);

通过多次调试，采用 block_size = 8 能够达到较快的速度。

运行结果为：

Correct
Custom: 13634.3 milliseconds
cuBLAS: 11508.2 milliseconds

此外，通过数组封装，让矩阵 B 在列方向的子块在内存中连续排列，能够进一步提高局部性。在代码中只需修改 _b 数组的内存排布。

#define _b(_i, _j, _x, _y) \
  _b[((_j) * grid_size + (_i)) * block_size * block_size + ((_y) * block_size + (_x))]

Shared Memory & Cooperative Fetching

计算目标矩阵 C 时，每一个线程块计算矩阵 C 的一个子块，有 \(C_{ij}=\sum _{k=0}^{N-1}A_{ik}B_{kj}\) 。

上面的做法中，每次都需要从 global memory 中拿取矩阵 A 和 B 中的元素，速度较慢。

在计算之前，将 \(A_{ik}\) 和 \(B_{kj}\) 放入 shared memory 中，计算时只需从 shared memory 中拿取元素，从而降低访存延迟。

#define a_shared(_x, _y) a_shared[(_x) * block_size + (_y)]
#define b_shared(_x, _y) b_shared[(_x) * block_size + (_y)]

/// \brief Do Matrix Multiplication on GPU.
__global__ void MultipleCudaKernel(const double *__restrict__ _a, 
                                     const double *__restrict__ _b, 
                                     double *__restrict__ result) 
{
  int grid_size = (size + block_size - 1) / block_size;

  __shared__ double a_shared[block_size * block_size];
  __shared__ double b_shared[block_size * block_size];

  const int i = blockIdx.x * block_size + threadIdx.x;
  const int j = blockIdx.y * block_size + threadIdx.y;
  const int x = threadIdx.x;
  const int y = threadIdx.y;

  double res = 0;
  for (int idx = 0; idx < gridDim.x; ++idx) {
    // Load matrix to shared memory
    a_shared(x, y) = _a(blockIdx.x, idx, x, y);
    b_shared(x, y) = _b(idx, blockIdx.y, x, y);
    __syncthreads();

    for (int k = 0; k < block_size; ++k) {
      res += a_shared(x, k) * b_shared(k, y);
    }
    __syncthreads();
  }
  if (i < size && j < size) {
    result(i, j) = res;
  }
}

运行结果为：

Correct
Custom: 17235.6 milliseconds
cuBLAS: 11489.1 milliseconds

性能有所下滑，推测是因为 bank conflict 较多，导致访存效率较低。

Bank Conflict

假设存储器有 16 个 bank ，且连续的 16 个矩阵元素被分别存储到 16 个 bank 中。

当每行元素在内存中连续时，bank 的分配如下图（其中绿色数字为元素所在 bank 编号），

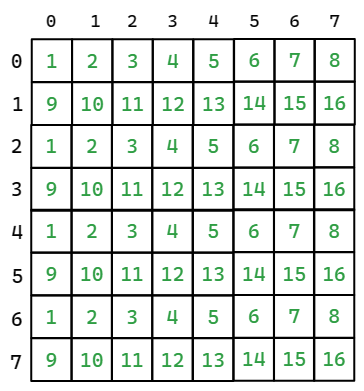
若 a_shared 采用如上的数据排布，则每个线程块对 a_shared 的访问如下图。

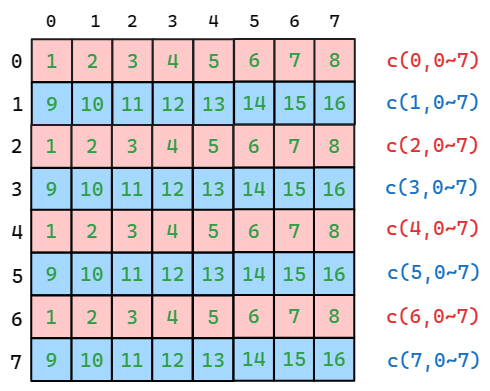
由于计算 c(x, 0~7) 时各个线程均访问相同的地址，通过广播则不会产生 bank conflict 。故主要产生 bank conflict 的原因是不同行的线程访问了同一 bank 的不同位置。

通过对内存进行重新配布，使得每一列的元素在内存中连续。如图，此时不同行的线程不会产生 bank conflict 。

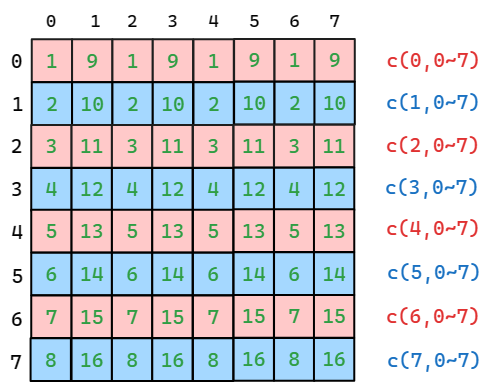
对于 b_shared 矩阵，同理可知让其每行元素在内存中连续，即可避免 bank conflict 。

代码中只需改动 a_shared 数组的内存分布：

#define a_shared(_x, _y) a_shared[(_y) * block_size + (_x)]

运行结果：

Correct
Custom: 11333.5 milliseconds
cuBLAS: 11484.9 milliseconds

以上部分的代码在 /code/baseline.cu 中，编译参数位于 /code/Makefile ，运行参数为

srun -p 2080Ti -N 1 -n 1 --cpus-per-task=8 --gpus=1 gemm

Tensor Core

使用 nvcuda::wmma 中的 Tensor Core API 调用 Tensor Core 进行矩阵乘法。

由于对于数据类型 double ，只提供了 8x8x4 的 Matrix Size ，故分块计算时，将 8x8x8 的矩阵乘法拆分成两次 8x8x4 的矩阵乘法，调用 Tensor Core 进行计算。

#define a_shared(_x, _y) a_shared[(_y) * block_size + (_x)]
#define b_shared(_x, _y) b_shared[(_x) * block_size + (_y)]
#define c_shared(_x, _y) c_shared[(_x) * block_size + (_y)]

/// \brief Do Matrix Multiplication on GPU.
__global__ void MultipleCudaKernel(const double *__restrict__ _a, 
                                     const double *__restrict__ _b, 
                                     double *__restrict__ result) 
{
  int grid_size = (size + block_size - 1) / block_size;

  __shared__ double a_shared[block_size * block_size];
  __shared__ double b_shared[block_size * block_size];
  __shared__ double c_shared[block_size * block_size];

  wmma::fragment<wmma::matrix_a, block_size, block_size, 
                block_size / 2, double, wmma::col_major> a_frag;
  wmma::fragment<wmma::matrix_b, block_size, block_size, 
                block_size / 2, double, wmma::row_major> b_frag;
  wmma::fragment<wmma::accumulator, block_size, block_size, 
                block_size / 2, double> c_frag;

  const int i = blockIdx.x * block_size + threadIdx.x;
  const int j = blockIdx.y * block_size + threadIdx.y;
  const int x = threadIdx.x;
  const int y = threadIdx.y;

  wmma::fill_fragment(c_frag, 0.0f);

  for (int idx = 0; idx < gridDim.x; ++idx) {
    a_shared(x, y) = _a(blockIdx.x, idx, x, y);
    b_shared(x, y) = _b(idx, blockIdx.y, x, y);
    __syncthreads();

    wmma::load_matrix_sync(a_frag, a_shared, block_size);
    wmma::load_matrix_sync(b_frag, b_shared, block_size);
    wmma::mma_sync(c_frag, a_frag, b_frag, c_frag);

    wmma::load_matrix_sync(a_frag, 
            a_shared + block_size * block_size / 2, block_size);
    wmma::load_matrix_sync(b_frag, 
            b_shared + block_size * block_size / 2, block_size);
    wmma::mma_sync(c_frag, a_frag, b_frag, c_frag);
    __syncthreads();
  }

  wmma::store_matrix_sync(c_shared, c_frag, 
                          block_size, wmma::mem_row_major);
  __syncthreads();

  if (i < size && j < size) {
    result(i, j) = c_shared(x, y);
  }
}

运行结果为：

Correct
Custom: 2127.59 milliseconds
cuBLAS: 899.045 milliseconds

Bonus 部分代码位于 /code_tensor/baseline.cu 中，编译参数位于 /code_tensor/Makefile 中，运行参数为：

srun -p A100 -N 1 -n 1 --cpus-per-task=8 --gpus=1 ./gemm

Reference

• How to optimize GEMM on CPU
• 深入浅出GPU优化系列：GEMM优化（一）
• 传统 CUDA GEMM 不完全指北
• 银河系CUDA编程指南(3)——矩阵乘法的分块实现
• CUDA C++ Programming Guide # Warp Matrix Functions