跳转至

Checkmate

Checkpoint Strategy

论文链接：Training Deep Nets with Sublinear Memory Cost

用时间换空间。将计算图分成 k 段，保存每段的输出，丢弃中间结果，反向传播时重新进行前向计算，再次得到中间结果。空间复杂度 \(O(n/k) + O(k)\)，取 \(k = \sqrt{n}\) 得 \(O(\sqrt{n})\)。

Checkmate

论文链接：Checkmate: Breaking the Memory Wall with Optimal Tensor Rematerialization

Introduction

深度学习训练过程需要大量的高带宽内存来存储中间激活值（activation tensors）。为了降低内存开销，已有的解决方案是通过丢弃部分 tensor，不存储进 RAM，在反向传播时重新计算这些 tensor（rematerialization）。然而现有的 rematerialization 方法是启发式的，并且只适用于 linear graph 或 path graph，无法处理非线性的 DNN 结构。

Checkmate 提出了一种基于 MILP（Mixed Integer Linear Programming 混合整数线性规划）的最优 rematerialization 方法，能够处理任意 DNN 网络结构。Checkmate 将 tensor rematerialization 问题建模为一个约束优化问题（constrained optimization problem），使用 gurobi 作为求解器，能够在合理的时间内找到最优解。

Motivation

提到 TensorFlow 和 PyTorch 都保存了所有的中间激活值（activation tensors），导致了巨大的内存开销。引入 rematerialization 策略能够显著降低内存使用。

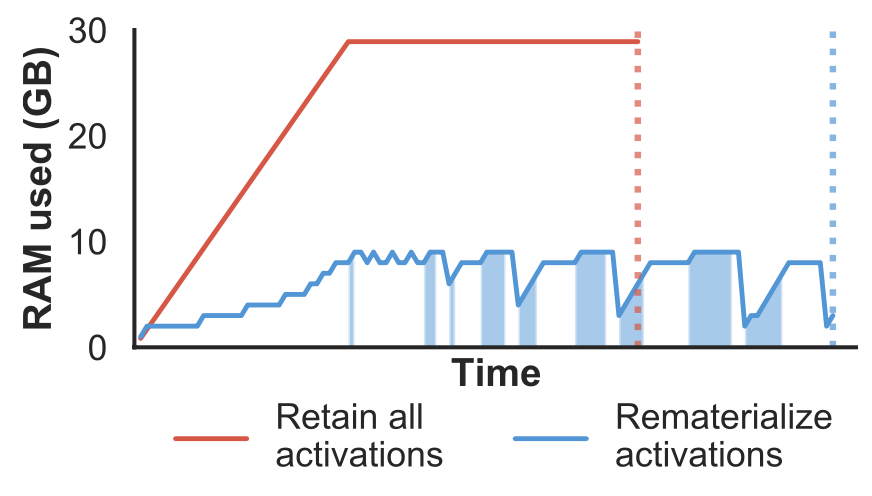
大多数 prior work 都假设网络有线性的计算图，比如 Training Deep Nets with Sublinear Memory Cost，线性图假设限制了算法的适用性。除此之外，prior work 还假设每一层进行 recompute 的代价都是相同的，但是对于部分架构，比如 VGG19，最复杂的层的计算代价可能远高于其他层。

Checkmate 对网络几乎没有任何假设，允许

  • 每个节点有任意多个输入和输出
  • 每层的内存成本可以不同
  • 每层的计算成本可以不同

仅需要节点的依赖关系在评估之前被确定，且在执行期间的任意时间点，需驻留在内存中的 tensor 必须可放入 RAM。

Checkpointing and rematerialization

Prior work 聚焦在理想情况下的线性 n 层网络的分段方式，使用简单的启发式方法来选择 checkpoint 的位置，然而实际情况中 DNN 每层的内存使用量和计算成本差异很大，导致启发式方法的效果不佳。另外有工作还提出了使用 DP 和分治的方法来优化 checkpoint 的选择。

另外还跟寄存器分配问题进行了类比，寄存器数量不足时，编译器可以将部分变量溢出存储到内存中，也可以舍弃部分变量，在需要时重新计算，编译器会在两种方法之间进行权衡。而 LLM 训练中，中间变量规模远大于传统的寄存器规模，将变量溢出存储到 RAM 的成本很大，因此，对中间激活值进行重新计算更为合适。

Reversible Networks

Gomez 等人提出了一种可逆（近似可逆）残差深度神经网络（DNN）架构，其中中间临时值可以根据标准前向计算得出的值重新计算。这种可逆性使得在反向传播时可以重新计算中间激活值，从而降低内存使用。相比之下，Rematerialization 可以节省更多成本，但可逆网络可以作为一种补充方法，适用于特定的网络架构和任务。

Distributed computation

分布式内存计算和梯度累积两种方法和 rematerialization 方法正交，能够在不同的层面上优化内存使用。然而，分布式内存计算（模型并行）需要访问额外的设备，以及需要快速的通信网络支持；梯度累积则会降低性能，在小批量训练下效果不佳。

Activation compression

在某些 DNN 训练中，在不损失太多精度的前提下，可以对部分数据进行压缩，比如处理数据集中的原始图像、对激活值进行量化等。这些方法可以有效降低内存使用，但会造成精度损失。Checkmate 则不会影响模型精度。

Optimal Rematerialization

将 Rematerialization 问题建模为 mixed integer linear program (MILP) 问题。

Problem definition

计算图 \(G=(V, E)\) 为包含 \(n\) 个节点 \(V=\{v_1, \dots, v_n\}\) 的有向无环图，其中每个节点表示产生值（例如中间激活值）的运算。\(E\) 表示运算之间的依赖关系。节点按拓扑序编号，使得运算 \(v_j\) 仅依赖运算 \(v_{i<j}\)。

每个运算的结果（输出）需要 \(M_v\) 的内存来存储，使用其输入对输出进行重新计算需要 \(C_v\) 的成本。目标是在内存预算 \(M_{\text{budget}}\) 下，最大化内存使用，最小化计算成本。

Representing a schedule

具体的 schedule 策略表示为每个节点保存在内存中或者进行重计算。将网络划分为 \(T\) 个阶段，每个阶段只允许一个节点重计算一次，定义：

  • \(S_{t, i} \in \{0, 1\}\) 表示运算 \(i\) 的结果从阶段 \(t - 1\) 直到阶段 \(t\) 都被保存在内存中。
  • \(R_{t, i} \in \{0, 1\}\) 表示运算 \(i\) 在阶段 \(t\) 进行重计算。

令 \(T = n\)。

Scheduling with ample memory

即使内存充足，仍需要保证运算在被重新计算时，其所有依赖都可用。优化问题：

\[ \begin{align} \arg\min_{R, S} & \quad \sum_{t=1}^{n} \sum_{i=1}^{t} C_i R_{t, i} \tag{1a} \\ \text{subject to} & \\ R_{t, j} & \leq R_{t, i} + S_{t, i}, \quad \forall t, \forall(v_i, v_j) \in E \tag{1b} \\ S_{t, i} & \leq R_{t-1, i} + S_{t-1, i}, \quad \forall t \geq 2, \forall i \tag{1c} \\ \sum_{i} S_{1, i} &= 0, \tag{1d} \\ \sum_{t} R_{t, n} & \leq 1, \tag{1e} \\ R_{t, i}, S_{t, i} & \in \{0, 1\}, \quad \forall t, i \tag{1f} \end{align} \]
  • （1a）：优化目标，最小化计算成本。
  • （1b）：若运算 \(j\) 在阶段 \(t\) 被重新计算，则其所有依赖 \(i\) 必须在阶段 \(t\) 可用（要么被重新计算，要么保存在内存中）。
  • （1c）：若运算 \(i\) 在阶段 \(t-1\) 到阶段 \(t\) 期间被保存在内存中，则运算 \(i\) 要么在阶段 \(t-1\) 被重新计算，要么在阶段 \(t-1\) 及之前已经保存在内存中。
  • （1d）：初始阶段不保存任何运算结果。
  • （1e）：最终的运算必须在某个阶段被计算，确保训练过程的完整性。
  • （1f）：决策变量 \(R, S\) 的定义。

Constraining memory utilization

引入变量 \(U_{t, k} \in \mathbb{R}_+\)，表示在阶段 \(t\) 中，运算 \(v_k\) 完成时所使用的内存。引入变量 \(\text{FREE}_{t, i, k} \in \{0, 1\}, (v_i, v_k) \in E\)，表示在阶段 \(t\) 中，运算 \(v_k\) 完成后，是否可以释放运算 \(v_i\) 占用的内存。

两个假设：

  1. 网络的输入和参数一直驻留在内存中。
  2. 有足够的空间存放参数梯度，参数梯度所占内存和参数所占内存相同。
  3. 在阶段开始时，所有 checkpointed value 都驻留在内存中。

递归定义 \(U_{t, k}\)：

\[ U_{t, 0} = M_{\text{input}} + 2M_{\text{param}} + \sum_{i=1}^{n} M_i S_{t, i} \tag{2} \]

即每个阶段开始前，所用内存为：输入所占内存、参数和参数梯度所占内存、以及所有前一阶段保存在 checkpoint 中的运算结果所占内存之和。

在计算节点 \(v_{k+1}\) 前，\(v_k\) 及其依赖节点若以后不再使用，则可以释放其占用的内存。则递归定义为

\[ U_{t, k+1} = U_{t, k} - \text{mem_freed}_t(v_k) + R_{t, k+1}M_{k+1} \tag{3} \]

\(\text{mem_freed}_t(v_k)\) 表示在阶段 \(t\) 中，运算 \(v_k\) 完成后，节点 \(v_k\) 及其依赖可被释放的内存。令

\[ \begin{align} \text{DEPS}[k] &= \{i \ : \ (v_i, v_k) \in E\} \\ \text{USERS}[i] &= \{j \ : \ (v_i, v_j) \in E\} \end{align} \]

则

\[ \begin{align} \text{mem_freed}_t(v_k) &= \sum_{i \in \text{DEPS}[k] \cup \{k\}} M_i \times \text{FREE}_{t, i, k} \tag{4} \\ \text{FREE}_{t, i, k} &= R_{t, k} (1 - S_{t+1, i}) \prod_{j \in \text{USERS}[i], j > k} (1 - R_{t, j}) \tag{5} \end{align} \]

式（5）确保：当 \(v_i\) 需要驻留在内存中时，不对其进行释放；当当前阶段存在 \(v_i\) 的子节点需要重计算时，不释放 \(v_i\) 的内存；当 \(v_k\) 不进行重计算时，不能保证 \(v_i\) 能被释放，由于每个阶段只有一个节点进行重计算，所以也保证了不会重复释放内存。

Linear reformulation of memory constraint

由于 \(\text{FREE}\) 的表达式不是线性的，不能放入 ILP 模型中，需要将其变换成线性形式。引入两个引理

Lemma 4.1 Linear Reformulation of Binary Polynomial

若 \(x_1, \dots, x_n \in \{0, 1\}\)，则

\[ \prod_{i=1}^n x_i = \begin{cases} 1 & \quad \sum_{i=1}^n (1-x_i) = 0 \\ 0 & \quad otherwise \end{cases} \]

Lemma 4.2 Linear Reformulation of Indicator Constraints

整数 \(y\)，存在常量上界 \(\kappa\)，即 \(0 \leq y \leq \kappa\)，则

\[ x = \begin{cases} 1 & \quad y = 0 \\ 0 & \quad otherwise \end{cases} \]

当且仅当 \(x \in \{0, 1\}, (1 - x) \leq y \leq \kappa(1 - x)\) 时成立。

令 \(\text{num_hazards}(t, i, k)\) 表示约束 (5) 中右侧为零的因子个数，则有

\[ \text{num_hazards}(t, i, k) = (1 - R_{t, k}) + S_{t+1, i} + \sum_{j \in \text{USERS}[i], j > k} R_{t, j} \]

应用 Lemma 4.1 得

\[ \text{FREE}_{t, i, k} = \begin{cases} 1 & \quad \text{num_hazards}(t, i, k) = 0 \\ 0 & \quad \text{otherwise} \end{cases} \tag{6} \]

设 \(\kappa\) 为 \(\text{num_hazards}(t, i, k)\) 的上界，应用 Lemma 4.2 得

\[ \begin{align} \text{FREE}_{t, i, k} &\in \{0, 1\} \tag{7a} \\ 1 - \text{FREE}_{t, i, k} &\leq \text{num_hazards}(t, i, k) \tag{7b} \\ \kappa (1 - \text{FREE}_{t, i, k}) &\geq \text{num_hazards}(t, i, k) \tag{7c} \end{align} \]

Tractability via frontier-advancing stages

给定计算图的一个执行顺序（拓扑序），将节点划分为 frontier-advancing stages，使得 \(v_i\) 在阶段 \(i\) 中首次被求值。用约束 (8a-8c) 替换 (1d, 1e)：

\[ \begin{align} R_{i, i} &= 1, \quad \forall i \tag{8a} \\ \sum_{i \geq t} S_{t, i} &= 0 \tag{8b} \\ \sum_{i > t} R_{t, i} &= 0 \tag{8c} \end{align} \]

其中：

  • (8a) 确保每个节点在其对应的阶段被计算。
  • (8b, 8c) 确保节点 \(v_i\) 在阶段 \(i\) 之前未被计算过。

这种约束更加严格，减少了可行集的大小，限制了搜索空间，缩短运行时间。

Complete Integer Linear Program formulation

完整的 MILP：

\[ \begin{align} \arg\min_{R, S, U, FREE} & \quad \sum_{t = 1}^n \sum_{i = 1}^t C_i R_{t, i} \\ \text{subject to} & \\ R_{t, j} & \leq R_{t, i} + S_{t, i}, \quad \forall t, \forall(v_i, v_j) \in E \tag{1b} \\ S_{t, i} & \leq R_{t-1, i} + S_{t-1, i}, \quad \forall t \geq 2, \forall i \tag{1c} \\ R_{t, i}, S_{t, i} & \in \{0, 1\}, \quad \forall t, i \tag{1f} \\ U_{t, 0} &= M_{\text{input}} + 2M_{\text{param}} + \sum_{i=1}^{n} M_i S_{t, i} \tag{2} \\ U_{t, k+1} &= U_{t, k} - \text{mem_freed}_t(v_k) + R_{t, k+1}M_{k+1} \tag{3} \\ \text{FREE}_{t, i, k} &\in \{0, 1\} \tag{7a} \\ 1 - \text{FREE}_{t, i, k} &\leq \text{num_hazards}(t, i, k) \tag{7b} \\ \kappa (1 - \text{FREE}_{t, i, k}) &\geq \text{num_hazards}(t, i, k) \tag{7c} \\ R_{i, i} &= 1, \quad \forall i \tag{8a} \\ \sum_{i \geq t} S_{t, i} &= 0 \tag{8b} \\ \sum_{i > t} R_{t, i} &= 0 \tag{8c} \\ U_{t, k} &\leq M_{\text{budget}}, \quad \forall t, k \end{align} \tag{9} \]

Constraints implied by optimality

注意到 \(\text{FREE}_{t, k, k} = 1\) 当且仅当 \(v_k\) 被计算后没有被使用，那么直接不计算 \(v_k\) 也是可行的，即 \(R_{t, k} = 0\)。因此直接固定 \(\text{FREE}_{t, k, k} = 0\)，此时式 (4) 可以改为

\[ \text{mem_freed}_t(v_k) = \sum_{i \in \text{DEPS}[k]} M_i \times \text{FREE}_{t, i, k} \]

这样减少了 \(|V|^2\) 个变量。

Generating an execution plan

根据计算图 \(G=(V, E)\) 和 MILP 的解 \((R, S, FREE)\)，生成执行计划 \(P=(s_1, \dots, s_k)\)，其中 \(s_i\) 代表计算操作或者释放内存。

Cost model

计算成本 \(C\) 在构建 MILP 之前确定，方法是在目标硬件上使用一系列随机输入对网络层进行性能分析。并且由于输入和输出大小已知，计算图中每个值的内存消耗都可以静态计算，计算出的内存消耗 \(M\) 用于构建内存约束。

Approximation

由于求解 ILP 是 NP-hard 的，对于大规模的神经网络，对 ILP 进行精确求解不可能。论文采用的方法是：

  1. 先采用在多项式时间内生成分数解的线性规划
  2. 采用两阶段舍入算法：利用分数解先舍入一部分变量为整数解，再计算剩余变量的最优解。

Relaxing integrality constraints

通过放宽变量的取值范围，将整数约束转化为线性约束，从而可以在多项式时间内求解，即令 \(R, S, FREE \in [0, 1]\)。

求得分数解 \(R^*, S^*\) 之后，可以使用随机舍入或者确定性舍入得出整数解。但是直接舍入后可能导致解违反了约束条件。

A two-phase rounding strategy

采用两阶段舍入策略：

Memory budget feasibility

算法 2 满足了条件 (1b, 1c, 1f, 8a)，但是可能不满足内存约束。解决方法是在求解 ILP 时，令 \(U_{t, k} \leq (1 - \epsilon)M_{\text{budget}}\)，预留总内存预算的余量。

Evaluation

研究以下问题：

  1. 使用重计算策略时，如何权衡内存占用和计算开销之间的关系？
  2. 使用重计算策略处理大规模输入是否可行？
  3. 如何才能逼近最优重计算策略？

将 checkmate 和启发式算法 baseline 进行对比，在所有内存预算下，最优重计算都能显著降低 baseline 的计算开销，并实现比以往更低的内存占用。

Baselines and generalizations

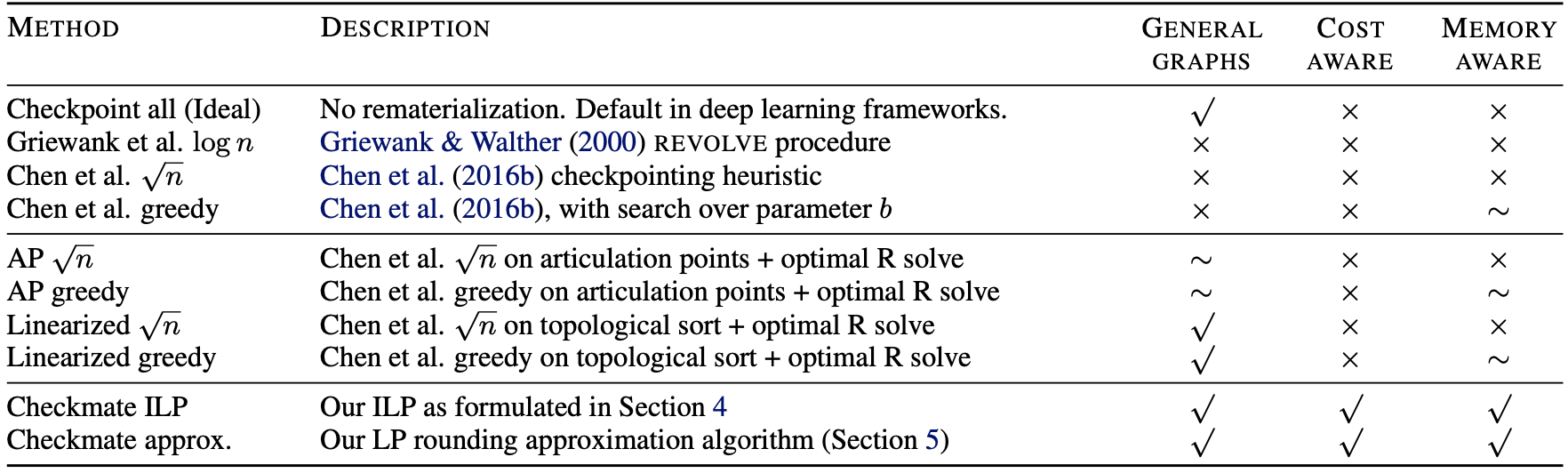
理想情况下（内存够用），Checkpoint all 保存所有中间结果，不进行重计算。

线性图中，可以直接使用 Griewank 等人提出的 \(\log n\) 算法和 Chen 等人提出的 \(\sqrt{n}\) 启发式算法和贪心算法。

对于非线性图，对 \(\sqrt{n}\) 启发式算法和贪心算法进行扩展，扩展得到 AP \(\sqrt{n}\) 算法、AP 贪心算法、线性化 \(\sqrt{n}\) 算法和线性化贪心算法。

Evaluation setup

Checkmate 使用 TensorFlow 实现，接受 Keras 模型作为输入。提取正向和反向计算图，使用 Gurobi 求解器求解优化问题 (9)。最后生成执行计划，构建静态训练图。

What is the trade-off between memory usage and computational overhead?

Checkmate 线性网络（VGG16、MobileNet）上以最低的计算成本生成内存限制内的解决方案，并显著降低复杂架构（U-Net）上的内存消耗和计算成本。

Are large inputs practical with rematerialization?

为 ILP 问题加入变量 \(B\) 表示 batchsize，添加约束再次求解，得出最大 batchsize。经过测试，checkmate 的最大 batchsize 在 U-Net、FCN8、SegNet、VGG19、ResNet50、MobileNet 几种模型中均高于 baseline，在部分模型（U-Net、MoblieNet）上提升显著。

How well can we approximate the optimal rematerialization policy?

测量了近似解与最优解的计算开销的比值，即最优解相对于近似解的加速比。对于所有测试模型，加速比最多为 \(1.06\times\)，说明近似解已经很接近最优解。

CONCLUSION

本文提出的 Checkmate 重计算策略，允许在有限的内存上训练大型神经网络。并且不需要对神经网络结构作出强假设，能够支持残差网络等复杂结构，并通过一个硬件感知、基于配置文件的 cost model 来评估整个计算图中非均匀内存使用和计算成本的影响。最佳的重计算策略在各种内存限制下都具有最小的计算开销，并且基于 Checkmate 能够训练具有显著更大批量大小的高分辨率模型。此外，论文还提出了一个两阶段舍入策略对 ILP 的最优解进行了近似，能够在多项式时间内获得接近最优的解。